


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-1-2021
Date: 30-4-2020
Date: 21-11-2020
|
The Lucas numbers are the sequence of integers  defined by the linear recurrence equation
defined by the linear recurrence equation
 |
(1) |
with 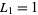 and
and 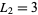 . The
. The 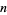 th Lucas number is implemented in the Wolfram Language as LucasL[n].
th Lucas number is implemented in the Wolfram Language as LucasL[n].
The values of 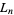 for
for 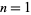 , 2, ... are 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, ... (OEIS A000204).
, 2, ... are 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, ... (OEIS A000204).
The Lucas numbers are also a Lucas sequence  and are the companions to the Fibonacci numbers
and are the companions to the Fibonacci numbers 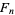 and satisfy the same recurrence.
and satisfy the same recurrence.
The number of ways of picking a set (including the empty set) from the numbers 1, 2, ..., 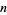 without picking two consecutive numbers (where 1 and
without picking two consecutive numbers (where 1 and 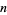 are now consecutive) is
are now consecutive) is 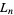 (Honsberger 1985, p. 122).
(Honsberger 1985, p. 122).
The only square numbers in the Lucas sequence are 1 and 4 (Alfred 1964, Cohn 1964). The only triangular Lucas numbers are 1, 3, and 5778 (Ming 1991). The only cubic Lucas number is 1.
Rather amazingly, if 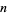 is prime,
is prime, 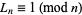 . The converse does not necessarily hold true, however, and composite numbers
. The converse does not necessarily hold true, however, and composite numbers 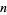 such that
such that 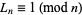 are known as Lucas pseudoprimes.
are known as Lucas pseudoprimes.
For 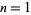 , 2, ..., the numbers of decimal digits in
, 2, ..., the numbers of decimal digits in 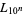 are 1, 3, 21, 209, 2090, 20899, 208988, 2089877, ... (OEIS A114469). As can be seen, the initial strings of digits settle down to produce the number 208987640249978733769..., which corresponds to the decimal digits of
are 1, 3, 21, 209, 2090, 20899, 208988, 2089877, ... (OEIS A114469). As can be seen, the initial strings of digits settle down to produce the number 208987640249978733769..., which corresponds to the decimal digits of 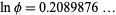 (OEIS A097348), where
(OEIS A097348), where 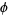 is the golden ratio. This follows from the fact that for any power function
is the golden ratio. This follows from the fact that for any power function 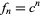 , the number of decimal digits for
, the number of decimal digits for 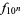 is given by
is given by 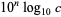 .
.
The lengths of the cycles for Lucas numbers (mod 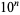 ) for
) for 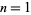 , 2, ... are 12, 60, 300, 3000, 30000, 300000, 300000, ... (OEIS A114307).
, 2, ... are 12, 60, 300, 3000, 30000, 300000, 300000, ... (OEIS A114307).
The analog of Binet's Fibonacci number formula for Lucas numbers is
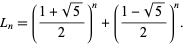 |
(2) |
Another formula is
![L_n=[phi^n]](https://mathworld.wolfram.com/images/equations/LucasNumber/NumberedEquation3.gif) |
(3) |
for 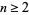 , where
, where 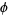 is the golden ratio and
is the golden ratio and ![[x]](https://mathworld.wolfram.com/images/equations/LucasNumber/Inline27.gif) denotes the nearest integer function.
denotes the nearest integer function.
Another recurrence relation for 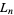 is given by,
is given by,
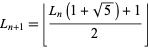 |
(4) |
for 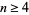 , where
, where 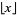 is the floor function.
is the floor function.
Additional identities satisfied by Lucas numbers include
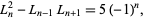 |
(5) |
and
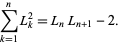 |
(6) |
The Lucas numbers obey the negation formula
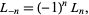 |
(7) |
the addition formula
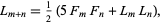 |
(8) |
where 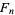 is a Fibonacci number, the subtraction formula
is a Fibonacci number, the subtraction formula
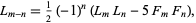 |
(9) |
the fundamental identity
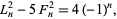 |
(10) |
conjugation relation
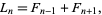 |
(11) |
successor relation
 |
(12) |
double-angle formula
 |
(13) |
multiple-angle recurrence
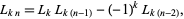 |
(14) |
multiple-angle formulas
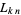 |
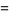 |
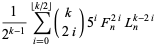 |
(15) |
 |
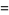 |
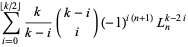 |
(16) |
 |
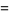 |
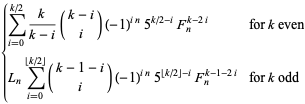 |
(17) |
 |
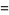 |
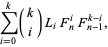 |
(18) |
product expansions
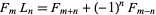 |
(19) |
and
![F_mF_n=1/5[L_(m+n)-(-1)^nL_(m-n)],](https://mathworld.wolfram.com/images/equations/LucasNumber/NumberedEquation16.gif) |
(20) |
square expansion,
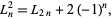 |
(21) |
and power expansion
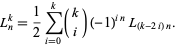 |
(22) |
The Lucas numbers satisfy the power recurrence
![sum_(j=0)^(t+1)(-1)^(j(j+1)/2)[t+1; j]_FL_(n-j)^t=0,](https://mathworld.wolfram.com/images/equations/LucasNumber/NumberedEquation19.gif) |
(23) |
where ![[a; b]_F](https://mathworld.wolfram.com/images/equations/LucasNumber/Inline44.gif) is a Fibonomial coefficient, the reciprocal sum
is a Fibonomial coefficient, the reciprocal sum
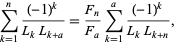 |
(24) |
the convolution
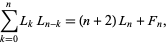 |
(25) |
the partial fraction decomposition
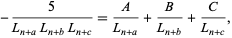 |
(26) |
where
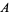 |
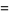 |
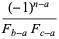 |
(27) |
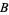 |
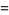 |
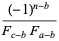 |
(28) |
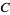 |
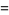 |
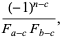 |
(29) |
and the summation formula
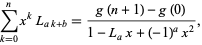 |
(30) |
where
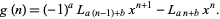 |
(31) |
Let 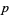 be a prime
be a prime 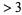 and
and 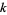 be a positive integer. Then
be a positive integer. Then 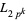 ends in a 3 (Honsberger 1985, p. 113). Analogs of the Cesàro identities for Fibonacci numbers are
ends in a 3 (Honsberger 1985, p. 113). Analogs of the Cesàro identities for Fibonacci numbers are
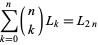 |
(32) |
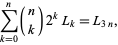 |
(33) |
where 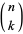 is a binomial coefficient.
is a binomial coefficient.
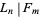 (
(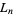 divides
divides 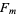 ) iff
) iff 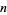 divides into
divides into 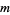 an even number of times.
an even number of times. 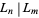 iff
iff 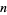 divides into
divides into 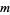 an odd number of times.
an odd number of times. 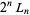 always ends in 2 (Honsberger 1985, p. 137).
always ends in 2 (Honsberger 1985, p. 137).
Defining
 |
(34) |
gives
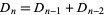 |
(35) |
(Honsberger 1985, pp. 113-114).
REFERENCES:
Alfred, Brother U. "On Square Lucas Numbers." Fib. Quart. 2, 11-12, 1964.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 94-101, 1987.
Brillhart, J.; Montgomery, P. L.; and Silverman, R. D. "Tables of Fibonacci and Lucas Factorizations." Math. Comput. 50, 251-260 and S1-S15, 1988.
Broadhurst, D. and Irvine, S. "Lucas Record." Post to primeform user forum. Jun. 19, 2006. https://groups.yahoo.com/group/primeform/message/7534.
Brown, J. L. Jr. "Unique Representation of Integers as Sums of Distinct Lucas Numbers." Fib. Quart. 7, 243-252, 1969.
Cohn, J. H. E. "Square Fibonacci Numbers, etc." Fib. Quart. 2, 109-113, 1964.
Dubner, H. and Keller, W. "New Fibonacci and Lucas Primes." Math. Comput. 68, 417-427 and S1-S12, 1999.
Guy, R. K. "Fibonacci Numbers of Various Shapes." §D26 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 194-195, 1994.
Hilton, P.; Holton, D.; and Pedersen, J. "Fibonacci and Lucas Numbers." Ch. 3 in Mathematical Reflections in a Room with Many Mirrors. New York: Springer-Verlag, pp. 61-85, 1997.
Hilton, P. and Pedersen, J. "Fibonacci and Lucas Numbers in Teaching and Research." J. Math. Informatique 3, 36-57, 1991-1992.
Hoggatt, V. E. Jr. The Fibonacci and Lucas Numbers. Boston, MA: Houghton Mifflin, 1969.
Honsberger, R. "A Second Look at the Fibonacci and Lucas Numbers." Ch. 8 in Mathematical Gems III. Washington, DC: Math. Assoc. Amer., 1985.
Koshy, T. Fibonacci and Lucas Numbers with Applications. New York: Wiley, 2001.
Leyland, P. ftp://sable.ox.ac.uk/pub/math/factors/lucas.Z
Lifchitz, H. and Lifchitz, R. "PRP Top Records." https://www.primenumbers.net/prptop/searchform.php?form=L(n).
Ming, L. "On Triangular Lucas Numbers." Applications of Fibonacci Numbers, Vol. 4 (Ed. G. E. Bergum, A. N. Philippou, and A. F. Horadam). Dordrecht, Netherlands: Kluwer, pp. 231-240, 1991.
Sloane, N. J. A. Sequences A000204/M2341, A001606/M0961, A005479/M2627, A068070, A097348, A114469, and A114307 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|