Pollard p-1 Factorization Method

A prime factorization algorithm which can be implemented in a single-step or double-step form. In the single-step version, a prime factor 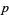 of a number  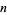can be found if  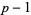is a product of small primes by finding an  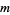such that

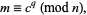where 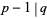, with  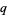a large number and 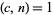. Then since 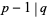, , 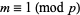so 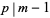. There is therefore a good chance that 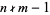, in which case  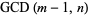(where GCD is the greatest common divisor) will be a nontrivial divisor of .

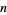In the double-step version, a prime factor 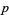 can be found if  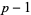is a product of small primes and a single larger prime.

REFERENCES:

Bressoud, D. M. Factorization and Primality Testing. New York: Springer-Verlag, pp. 67-69, 1989.

Pollard, J. M. "Theorems on Factorization and Primality Testing." Proc. Cambridge Phil. Soc. 76, 521-528, 1974.