


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-12-2020
Date: 8-10-2020
Date: 14-4-2020
|
A primality test is a test to determine whether or not a given number is prime, as opposed to actually decomposing the number into its constituent prime factors (which is known as prime factorization).
Primality tests come in two varieties: deterministic and probabilistic. Deterministic tests determine with absolute certainty whether a number is prime. Examples of deterministic tests include the Lucas-Lehmer test and elliptic curve primality proving. Probabilistic tests can potentially (although with very small probability) falsely identify a composite number as prime (although not vice versa). However, they are in general much faster than deterministic tests. Numbers that have passed a probabilistic prime test are therefore properly referred to as probable primes until their primality can be demonstrated deterministically.
A number that passes a probabilistic test but is in fact composite is known as a pseudoprime. There are many specific types of pseudoprimes, the most common being the Fermat pseudoprimes, which are composites that nonetheless satisfy Fermat's little theorem.
The Rabin-Miller strong pseudoprime test is a particularly efficient test. The Wolfram Language implements the multiple Rabin-Miller test in bases 2 and 3 combined with a Lucas pseudoprime test as the primality test used by the function PrimeQ[n]. Like many such algorithms, it is a probabilistic test using pseudoprimes. In order to guarantee primality, a much slower deterministic algorithm must be used. However, no numbers are actually known that pass advanced probabilistic tests (such as Rabin-Miller) yet are actually composite.
The state of the art in deterministic primality testing for arbitrary numbers is elliptic curve primality proving. As of Feb. 2009, the largest number certified by the program PRIMO (7993 decimal digits) took eight months on a 2-GHz processor.
Unlike prime factorization, primality testing was long believed to be a P-problem (Wagon 1991). This had not been demonstrated, however, until Agrawal et al. (2002) unexpectedly discovered a polynomial time algorithm for primality testing that has asymptotic complexity of 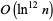 (Bernstein 2002, Clark 2002, Indian Institute of Technology 2002, Pomerance 2002ab, Robinson 2002). Their algorithm has come to be called the AKS primality test.
(Bernstein 2002, Clark 2002, Indian Institute of Technology 2002, Pomerance 2002ab, Robinson 2002). Their algorithm has come to be called the AKS primality test.
REFERENCES:
Agrawal, M.; Kayal, N.; and Saxena, N. "Primes in P." Preprint, Aug. 6, 2002. https://www.cse.iitk.ac.in/primality.pdf.
Bernstein, D. J. "An Exposition of the Agrawal-Kayal-Saxena Primality-Proving Theorem." 2002. https://cr.yp.to/papers/aks.ps.
Beauchemin, P.; Brassard, G.; Crépeau, C.; Goutier, C.; and Pomerance, C. "The Generation of Random Numbers that are Probably Prime." J. Crypt. 1, 53-64, 1988.
Brillhart, J.; Lehmer, D. H.; Selfridge, J.; Wagstaff, S. S. Jr.; and Tuckerman, B. Factorizations of b-n+/-1, b=2, 3, 5, 6, 7, 10, 11, 12 Up to High Powers, rev. ed. Providence, RI: Amer. Math. Soc., pp. lviii-lxv, 1988.
Clark, E. "Polynomial Time Primality Test." sci.math newsgroup posting. 6 Aug 2002.
Cohen, H. and Lenstra, A. K. "Primality Testing and Jacobi Sums." Math. Comput. 42, 297-330, 1984.
Indian Institute of Technology. "PRIMES is in P." https://www.cse.iitk.ac.in/news/primality.html.
Kayal, N. and Saxena, N. "Towards a Deterministic Polynomial-Time Test." Technical Report. Kanpur, India: Indian Institute of Technology, 2002. https://www.cse.iitk.ac.in/research/btp2002/primality.html.
Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd ed. Reading, MA: Addison-Wesley, 1998.
Martin, M. "PRIMO--Primality Proving." https://www.ellipsa.net/public/primo/primo.html.
Martin, M. "PRIMO Record." https://www.ellipsa.net/public/primo/record.html.
Pomerance, C. "RE: New Polynomial Time Primality Test?" 7 Aug 2002a. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0208&L=nmbrthry&P=956.
Pomerance, C. "A New Primal Screen." FOCUS: Newsletter of the Math. Assoc. Amer. 22, No. 8, 4-5, 2002b.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, 1994.
Robinson, S. "New Method Said to Solve Key Problem in Math." New York Times, p. A16, August 8, 2002.
Wagon, S. "Primality Testing." Math. Intell. 8, No. 3, 58-61, 1986.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 15-17, 1991.
Weisstein, E. W. "Primality Testing Is Easy." MathWorld Headline News, Aug. 7, 2002. https://mathworld.wolfram.com/news/2002-08-07/primetest/.
Williams, H. C. Edouard Lucas and Primality Testing. New York: Wiley, 1998.



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
مكتب السيد السيستاني يعزي أهالي الأحساء بوفاة العلامة الشيخ جواد الدندن
|
|
|