المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Wolstenholme Prime |
 548
 05:46 مساءً
date: 31-8-2020 |
Author : Sloane, N. J. A 
Book or Source : Sequence A088164 in "The On-Line Encyclopedia of Integer Sequences." 
Page and Part : ...|
Read More
Date: 28-7-2020
543
Date: 26-9-2020
570
Date: 18-10-2020
565
|
A prime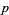 
is called a Wolstenholme prime if the central binomial coefficient
 |
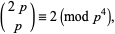(1) |
or equivalently if
 |
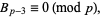(2) |
where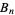 
is the 
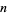th Bernoulli number and the congruence is fractional.
A prime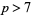 
is a Wolstenholme prime if and only if
 |
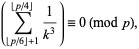(3) |
where the congruence is again fractional.
The only known Wolstenholme primes are 16843 and 2124679 (OEIS A088164). There are no others up to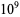 
(McIntosh 2004).
REFERENCES:
McIntosh, R. email to Paul Zimmermann. 9 Mar 2004. https://www.loria.fr/~zimmerma/records/Wieferich.status.
Sloane, N. J. A. Sequence A088164 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
