


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-11-2020
Date: 24-10-2020
Date: 20-1-2021
|
A modification of Legendre's formula for the prime counting function 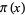 . It starts with
. It starts with
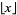 |
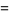 |
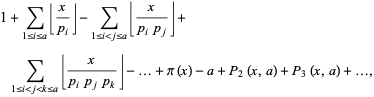 |
(1) |
where 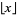 is the floor function,
is the floor function, 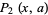 is the number of integers
is the number of integers 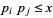 with
with 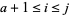 , and
, and 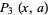 is the number of integers
is the number of integers 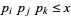 with
with 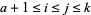 , and so on.
, and so on.
Identities satisfied by the 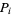 s include
s include
![P_2(x,a)=sum[pi(x/(p_i))-(i-1)]](https://mathworld.wolfram.com/images/equations/MeisselsFormula/NumberedEquation1.gif) |
(2) |
for 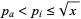 and
and
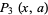 |
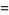 |
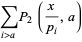 |
(3) |
 |
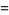 |
![sum_(i=a+1)^(c)sum_(j=i)^(pi(sqrt(x/p_i)))[pi(x/(p_ip_j))-(j-1)].](https://mathworld.wolfram.com/images/equations/MeisselsFormula/Inline19.gif) |
(4) |
Meissel's formula is
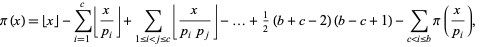 |
(5) |
where
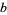 |
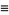 |
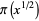 |
(6) |
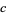 |
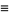 |
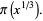 |
(7) |
Taking the derivation one step further yields Lehmer's formula.
REFERENCES:
Gram, J. "Rapport sur quelques calculs entrepris par M. Bertelsen et concernant les nombres premiers." Acta Math. 17, 301-314, 1893.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, p. 46, 1999.
Mathews, G. B. Ch. 10 in Theory of Numbers. New York: Chelsea, 1961.
Meissel, E. D. F. "Berechnung der Menge von Primzahlen, welche innerhalb der ersten Milliarde naturlicher Zahlen vorkommen." Math. Ann. 25, 251-257, 1885.
Riesel, H. "Meissel's Formula." Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 12-13, 1994.
Séroul, R. "Meissel's Formula." §8.7.3 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 179-181, 2000.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|