


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-12-2020
Date: 1-10-2020
Date: 6-1-2020
|
By analogy with the divisor function 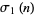 , let
, let
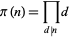 |
(1) |
denote the product of the divisors 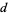 of
of 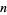 (including
(including 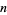 itself). For
itself). For 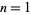 , 2, ..., the first few values are 1, 2, 3, 8, 5, 36, 7, 64, 27, 100, 11, 1728, 13, 196, ... (OEIS A007955).
, 2, ..., the first few values are 1, 2, 3, 8, 5, 36, 7, 64, 27, 100, 11, 1728, 13, 196, ... (OEIS A007955).
The divisor product satisfies the identity
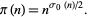 |
(2) |
The following table gives values of 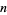 for which
for which 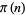 is a
is a 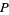 th power. Lionnet (1879) considered the case
th power. Lionnet (1879) considered the case 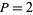 .
.
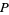 |
OEIS | 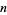 |
| 2 | A048943 | 1, 6, 8, 10, 14, 15, 16, 21, 22, 24, 26, ... |
| 3 | A048944 | 1, 4, 8, 9, 12, 18, 20, 25, 27, 28, 32, ... |
| 4 | A048945 | 1, 24, 30, 40, 42, 54, 56, 66, 70, 78, ... |
| 5 | A048946 | 1, 16, 32, 48, 80, 81, 112, 144, 162, ... |
Write the prime factorization of a number 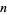 ,
,
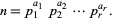 |
(3) |
Then the power of 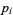 occurring in
occurring in 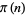 is
is
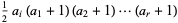 |
(4) |
(Kaplansky 1999). This allows rules for determining when 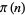 is a power of
is a power of 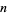 to be determined, as considered by Halcke (1719) and Lionnet (1879). Let
to be determined, as considered by Halcke (1719) and Lionnet (1879). Let 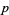 ,
, 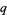 , and
, and 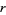 be distinct primes, then the following table gives the conditions and first few
be distinct primes, then the following table gives the conditions and first few 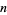 for which
for which 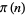 is a given power
is a given power 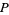 of
of 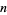 (Ireland and Rosen 1990, Kaplansky 1999, Dickson 2005). The case of third powers corresponds to numbers having exactly six divisors, the case of forth powers to numbers having eight divisors, and so on.
(Ireland and Rosen 1990, Kaplansky 1999, Dickson 2005). The case of third powers corresponds to numbers having exactly six divisors, the case of forth powers to numbers having eight divisors, and so on.
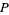 |
forms | Sloane | 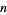 |
| 2 | 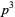 , , 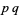 |
A007422 | 6, 8, 10, 14, 15, 21, 22, ... |
| 3 | 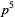 , , 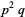 |
A030515 | 12, 18, 20, 28, 32, 44, ... |
| 4 | 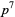 , , 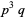 , , 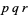 |
A030626 | 24, 30, 40, 42, 54, 56, ... |
| 5 | 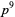 , , 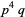 |
A030628 | 48, 80, 112, 162, 176, ... |
REFERENCES:
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, p. 58, 2005.
Halcke, P. Exs. 150-152 in Deliciae Mathematicae; oder, Mathematisches sinnen-confect. Hamburg, Germany: N. Sauer, p. 197, 1719.
Ireland, K. and Rosen, M. A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, p. 19, 1990.
Kaplansky, I. "The First Two Chapters of Dickson's History." Unpublished manuscript, Apr. 1999.
Lionnet, E. "Note sur les nombres parfaits." Nouv. Ann. Math. 18, 306-308, 1879.
Lucas, E. Ex. 6 in Théorie des nombres. Paris: Gauthier-Villars, p. 373, 1891.
Sloane, N. J. A. Sequences A000040/M0652, A007422/M4068, A007955, A030515, A030626, A030628, A048943, A048944, A048945, and A048946 in "The On-Line Encyclopedia of Integer Sequences."
Smarandache, F. Only Problems, Not Solutions!, 4th ed. Phoenix, AZ: Xiquan, 1993.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
ندوات وأنشطة قرآنية مختلفة يقيمها المجمَع العلمي في محافظتي النجف وكربلاء
|
|
|