Chebyshev's Theorem

There are at least two theorems known as Chebyshev's theorem.

The first is Bertrand's postulate, proposed by Bertrand in 1845 and proved by Chebyshev using elementary methods in 1850 (Derbyshire 2004, p. 124).

The second is a weak form of the prime number theorem stating that the order of magnitude of the prime counting function 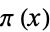 is

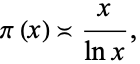where 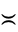 denotes "is asymptotic to" (Hardy and Wright 1979, p. 9). More precisely, Chebyshev showed in 1849 that if

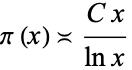for some constant 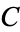, then  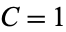(Derbyshire 2004, p. 123).

REFERENCES:

Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.