المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
Bilingual learners
2025-03-31
Cultural issues and schools Conclusion
2025-03-31
Asylum seekers
2025-03-31
Travellers in Britain
2025-03-31
Culture, language and learning
2025-03-31
Aiming high: raising the achievement of minority ethnic pupils (2003)
2025-03-31

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
ارسال الحسن (عليه السلام) إلى الكوفة
19-10-2015
Usage of MoS2
24-12-2018
إشاراتٌ عابرة وإلماعاتٌ خاطفة عن غياهب الوجود
5-11-2014
شبرنكوف ، بافيل الكسيفتش
12-11-2015
Primality Test
2-9-2020
إسماعيل بن أبي خالد.
28-12-2016

Hasse,s Resolution Modulus Theorem  
  
734   05:17 مساءً   date: 13-8-2020
Author : Cohn, H
Book or Source : Advanced Number Theory. New York: Dover
Page and Part : pp. 35-36


Read More
Pi Digits
Date: 10-3-2020 2759
Star Number
Date: 22-12-2020 851
Langlands Reciprocity
Date: 21-12-2019 737

Hasse's Resolution Modulus Theorem

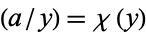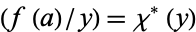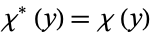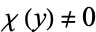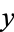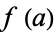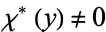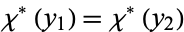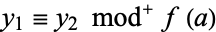The Jacobi symbol (a/y)=chi(y) as a number theoretic character can be extended to the Kronecker symbol (f(a)/y)=chi^*(y) so that chi^*(y)=chi(y) whenever chi(y)!=0. When y is relatively prime to f(a), then chi^*(y)!=0, and for nonzero values chi^*(y_1)=chi^*(y_2) iff y_1=y_2 mod^+ f(a). In addition, 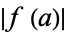|f(a)| is the minimum value for which the latter congruence property holds in any extension symbol for chi(y).

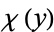REFERENCES:

Cohn, H. Advanced Number Theory. New York: Dover, pp. 35-36, 1980.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
الصين.. طريقة لمنع تطور قصر النظر لدى تلاميذ المدارس
التاريخ / 2025-03-28

الأخبار العلمية
ماذا سيحدث خلال كسوف الشمس يوم السبت؟
التاريخ / 2025-03-28

الساحة الاسلامية
قسم الشؤون الدينية يختتم محاضراته الرمضانية في صحن مرقد أبي الفضل العباس (عليه السلام)
التاريخ / 2025-03-30