


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-12-2020
Date: 17-8-2020
Date: 6-10-2020
|
The smallest composite squarefree number (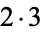 ), and the third triangular number (
), and the third triangular number (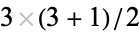 ). It is the also smallest perfect number, since
). It is the also smallest perfect number, since 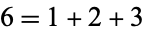 . The number 6 arises in combinatorics as the binomial coefficient
. The number 6 arises in combinatorics as the binomial coefficient 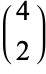 , which appears in Pascal's triangle and counts the 2-subsets of a set with 4 elements. It is also equal to
, which appears in Pascal's triangle and counts the 2-subsets of a set with 4 elements. It is also equal to 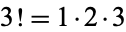 (3 factorial), the number of permutations of three objects, and the order of the symmetric group
(3 factorial), the number of permutations of three objects, and the order of the symmetric group 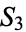 (which is the smallest non-Abelian group).
(which is the smallest non-Abelian group).
Six is indicated by the Latin prefix sex-, as in sextic, or by the Greek prefix hexa- (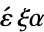 -), as in hexagon, hexagram, or hexahedron.
-), as in hexagon, hexagram, or hexahedron.
The six-fold symmetry is typical of crystals such as snowflakes. A mathematical and physical treatment can be found in Kepler (Halleux 1975), Descartes (1637), Weyl (1952), and Chandrasekharan (1986).
REFERENCES:
Chandrasekharan, K. Hermann Weyl (1885-1985): Centenary Lectures. Berlin: Springer-Verlag, 1986.
Descartes, R. Discours de la méthode: Les météores. Leyden, Netherlands, 1637.
Kepler, J. Étrenne ou la Neige sexangulaire. Translated from Latin by R. Halleux. Paris, France: J. Vrin Éditions du CNRS, 1975.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 67-69, 1986.
Weyl, H. Symmetry. Princeton, NJ: Princeton University Press, 1952.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|