عدد المواضيع في هذا القسم 9761 موضوعاً

تاريخ الرياضيات

الرياضيات المتقطعة

الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات

الهندسة

التفاضل و التكامل

المعادلات التفاضلية و التكاملية

التحليل

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان

Untitled Document

أبحث عن شيء أخر

أضيف حديثاً

النابذون ولاية محمد واله وراء ظهورهم لهم عذاب اليم

ماشية اللحم كالميك في القوقاز Kalmyk breed

العباءة العربية .. إرث الآباء واعتزاز الأبناء

التاريخ / 20-09-2024

مختارات

منتجات الالبان عالية الدهن

17-8-2016

الوساوس.

2024-01-16

مرض المسكردين الذي يصيب دودة الحرير

25-11-2015

مستوى قاعدي ( أساسي ) basal plane

26-12-2017

وجوب البعثة

3-08-2015

ما هو التجمع للنوم في الحشرات؟

19-2-2021

Leudesdorf Theorem

934

09:39 صباحاً date: 30-6-2020

Author : Hardy, G. H. and Wright, E. M.

Book or Source : "A Theorem of Leudesdorf." §8.7 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press

Page and Part : pp. 100-102

Euler Quartic Conjecture

Date: 26-5-2020

751

Decimal

Date: 23-11-2019

576

Subtraction

Date: 20-10-2019

776

Leudesdorf Theorem

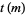Let t(m) denote the set of the 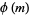phi(m) numbers less than and relatively prime to 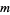, where 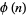phi(n) is the totient function. Then if

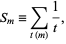(1)

then

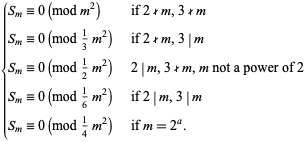${S_m=0 (mod m^2) if 2m, 3m; S_m=0 (mod 1/3m^2) if 2m, 3|m; S_m=0 (mod 1/2m^2) 2|m, 3m, m not a power of 2; S_m=0 (mod 1/6m^2) if 2|m, 3|m; S_m=0 (mod 1/4m^2) if m=2^a.$

(2)

REFERENCES:

Hardy, G. H. and Wright, E. M. "A Theorem of Leudesdorf." §8.7 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 100-102, 1979.

الجَــبْــر Algebra

الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.

علم المثلثات : Trigonometry

يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

المعادلات التفاضلية والتكاملية Differential equations and equations integrative

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.