Euler Quartic Conjecture

Euler (1772ab) conjectured that there are no positive integer solutions to the quartic Diophantine equation

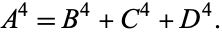This conjecture was disproved by Elkies (1988), who found an infinite class of solutions.

REFERENCES:

Berndt, B. C. and Bhargava, S. "Ramanujan--For Lowbrows." Amer. Math. Monthly 100, 644-656, 1993.

Clay Mathematics Institute. "Birch and Swinnerton-Dyer Conjecture." https://www.claymath.org/millennium/Birch_and_Swinnerton-Dyer_Conjecture/.

Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, p. 648, 2005.

Dutch, S. "Power Page: Euler's Conjecture." https://www.uwgb.edu/dutchs/RECMATH/rmpowers.htm#eulercon.

Elkies, N. "On 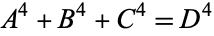." Math. Comput. 51, 825-835, 1988.

Euler, L. Commentationes Arithmeticae 1, xxxiii, No. 1, 1772a.

Euler, L. Commentationes Arithmeticae 2, lxviii, No. 3, 1772b.

Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 139-140, 1994.

Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, p. 201, 1998.

Jacobi, L. W. and Madden D. J. "On 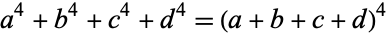." Amer. Math. Monthly 115, 220-236, 2008.

Lander, L. J.; Parkin, T. R.; and Selfridge, J. L. "A Survey of Equal Sums of Like Powers." Math. Comput. 21, 446-459, 1967.

Ward, M. "Euler's Problem on Sums of Three Fourth Powers." Duke Math. J. 15, 827-837, 1948.