


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-12-2020
Date: 5-1-2021
Date: 10-4-2020
|
Diophantus's riddle is a poem that encodes a mathematical problem. In verse, it read as follows:
'Here lies Diophantus,' the wonder behold. Through art algebraic, the stone tells how old: 'God gave him his boyhood one-sixth of his life, One twelfth more as youth while whiskers grew rife; And then yet one-seventh ere marriage begun; In five years there came a bouncing new son. Alas, the dear child of master and sage After attaining half the measure of his father's life chill fate took him. After consoling his fate by the science of numbers for four years, he ended his life.'
Stated in prose, the poem says that Diophantus's youth lasts 1/6 of his life. He grew a beard after 1/12 more of his life. After 1/7 more of his life, Diophantus married. Five years later, he had a son. The son lived exactly half as long as his father, and Diophantus died just four years after his son's death. All of this totals the years Diophantus lived.
Let 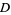 be the number of years Diophantus lived, and let
be the number of years Diophantus lived, and let 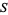 be the number of years his son lived. Then the above word problem gives the two equations
be the number of years his son lived. Then the above word problem gives the two equations
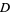 |
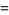 |
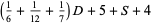 |
(1) |
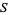 |
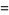 |
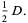 |
(2) |
Solving this simultaneously gives 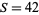 as the age of the son and
as the age of the son and 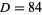 as the age of Diophantus.
as the age of Diophantus.
REFERENCES:
Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, pp. 186-187, 1998.
Pappas, T. "Diophantus' Riddle." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 123 and 232, 1989.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|