


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-12-2020
Date: 13-11-2019
Date: 8-10-2020
|
An NSW number (named after Newman, Shanks, and Williams) is an integer 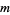 that solves the Diophantine equation
that solves the Diophantine equation
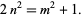 |
(1) |
In other words, the NSW numbers 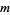 index the diagonals of squares of side length
index the diagonals of squares of side length 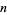 having the property that the squares of the diagonal
having the property that the squares of the diagonal 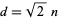 equals one plus a square number
equals one plus a square number 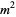 . Such numbers were called "rational diagonals" by the Greeks (Wells 1986, p. 70). The name "NSW number" derives from the names of the authors of the paper on the subject written by Newman et al. (1980/81).
. Such numbers were called "rational diagonals" by the Greeks (Wells 1986, p. 70). The name "NSW number" derives from the names of the authors of the paper on the subject written by Newman et al. (1980/81).
The first few NSW numbers are therefore 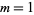 , 7, 41, 239, 1393, ... (OEIS A002315), which correspond to square side lengths
, 7, 41, 239, 1393, ... (OEIS A002315), which correspond to square side lengths 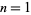 , 5, 29, 169, 985, 5741, 33461, 195025, ... (OEIS A001653). The values indexed by
, 5, 29, 169, 985, 5741, 33461, 195025, ... (OEIS A001653). The values indexed by 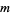 and
and 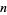 therefore give 2, 50, 1682, 57122, ... (OEIS A088920).
therefore give 2, 50, 1682, 57122, ... (OEIS A088920).
Taking twice the NSW numbers gives the sequence 2, 14, 82, 478, 2786, 16238, ... (OEIS A077444), which is exactly every other Pell-Lucas number.
The first few prime NSW numbers are 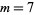 , 41, 239, 9369319, 63018038201, 489133282872437279, ... (OEIS A088165), corresponding to indices
, 41, 239, 9369319, 63018038201, 489133282872437279, ... (OEIS A088165), corresponding to indices 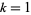 , 2, 3, 9, 14, 23, 29, 81, 128, 210, 468, 473, 746, 950, 3344, 4043, 4839, 14376, 39521, 64563, 72984, 82899, 84338, 85206, 86121, ... (OEIS A113501).
, 2, 3, 9, 14, 23, 29, 81, 128, 210, 468, 473, 746, 950, 3344, 4043, 4839, 14376, 39521, 64563, 72984, 82899, 84338, 85206, 86121, ... (OEIS A113501).
The following table summarizes the largest known NSW primes, where the indices 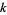 correspond via
correspond via 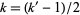 to the indices
to the indices 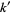 of prime half-Pell-Lucas numbers that are odd.
of prime half-Pell-Lucas numbers that are odd.
 |
decimal digits | discoverer | date |
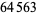 |
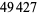 |
E. W. Weisstein | May 19, 2006 |
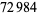 |
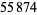 |
E. W. Weisstein | Aug. 29, 2006 |
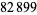 |
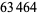 |
E. W. Weisstein | Nov. 16, 2006 |
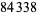 |
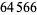 |
E. W. Weisstein | Nov. 26, 2006 |
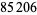 |
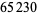 |
E. W. Weisstein | Dec. 10, 2006 |
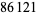 |
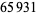 |
E. W. Weisstein | Jan. 25, 2007 |
Interestingly, the values 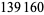 give every other convergent to Pythagoras's constant
give every other convergent to Pythagoras's constant 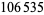 .
.
Explicit formula for 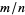 and
and 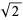 are given by
are given by
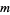 |
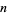 |
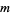 |
(2) |
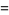 |
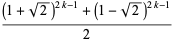 |
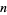 |
(3) |
for positive integers 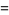 (Ribenboim 1996, p. 367). A recurrence relation for
(Ribenboim 1996, p. 367). A recurrence relation for 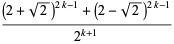 is given by
is given by
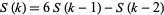 |
(4) |
with 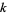 and
and 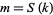 .
.
REFERENCES:
Newman, M.; Shanks, D.; and Williams, H. C. "Simple Groups of Square Order and an Interesting Sequence of Primes." Acta Arith. 38, 129-140, 1980/81.
Ribenboim, P. "The NSW Primes." §5.9 in The New Book of Prime Number Records. New York: Springer-Verlag, pp. 367-369, 1996.
Sloane, N. J. A. Sequences A001653/M3955, A002315/M4423, A077444, A088165, A088920, and A113501 in "The On-Line Encyclopedia of Integer Sequences."
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 70, 1986.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|