
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-8-2020
Date: 3-2-2020
Date: 6-5-2020
|
A Woodall number is a number of the form
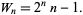 |
Woodall numbers are therefore similar to Mersenne numbers 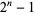 but with an additional factor of
but with an additional factor of 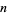 multiplying the power of 2, and to Cullen numbers
multiplying the power of 2, and to Cullen numbers 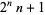 but with the sign flipped.
but with the sign flipped.
For 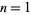 , 2, ..., the first few Woodall numbers are 1, 7, 23, 63, 159, 383, ... (OEIS A003261).
, 2, ..., the first few Woodall numbers are 1, 7, 23, 63, 159, 383, ... (OEIS A003261).
A Woodall number that is prime is known as a Woodall prime.
REFERENCES:
Cunningham, A. J. C. and Woodall, H. J. "Factorisation of 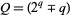 and
and 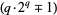 ." Messenger Math. 47, 1-38, 1917.
." Messenger Math. 47, 1-38, 1917.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 360-361, 1996.
Sloane, N. J. A. Sequence A003261/M4379 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|