المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Harmonic Expansion |
 674
 05:05 مساءً
date: 4-5-2020 |
Author : Sloane, N. J. A. 
Book or Source : Sequences A054977, A075874, and A096622 in "The On-Line Encyclopedia of Integer Sequences." 
Page and Part : ...|
Read More
Date: 26-1-2021
1828
Date: 19-1-2021
1375
Date: 31-1-2020
1079
|
A harmonic series is a continued fraction-like series ![[n;a,b,c,...]](https://mathworld.wolfram.com/images/equations/HarmonicExpansion/Inline1.gif)
defined by
 |
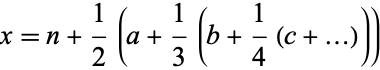(Havil 2003, p. 99).
Examples are given in the following table.
 |
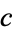OEIS | harmonic expansion |
 |
A054977 | [2, 1, 1, 1, 1, 1, 1, ...] |
 |
A096622 | [0, 1, 0, 1, 4, 1, 4, ...] |
 |
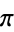A075874 | [3, 0, 0, 3, 1, 5, 6, 5, ...] |
REFERENCES:
Havil, J. "Harmonic Expansion." §11.8 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 98-100, 2003.
Sloane, N. J. A. Sequences A054977, A075874, and A096622 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
وفد كلية الزراعة في جامعة كربلاء يشيد بمشروع الحزام الأخضر
|
|
|
