Peg

The answer to the question "which fits better, a round peg in a square hole, or a square peg in a round hole?" can be interpreted as asking which is larger, the ratio of the area of a circle to its circumscribed square, or the area of the square to its circumscribed circle? In two dimensions, the ratios are  and , respectively. Therefore, a round peg fits better into a square hole than a square peg fits into a round hole (Wells 1986, p. 74).

However, this result is true only in dimensions 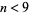, and for 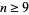, the unit 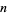-hypercube fits more closely into the 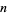-hypersphere than vice versa (Singmaster 1964; Wells 1986, p. 74). This can be demonstrated by noting that the formulas for the content  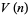of the unit 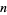-ball, the content  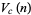of its circumscribed hypercube, and the content  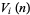of its inscribed hypercube are given by

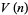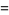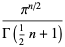			(1)
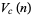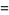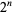			(2)
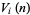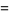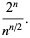			(3)

The ratios in question are then

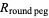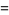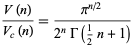			(4)
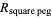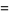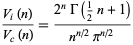			(5)

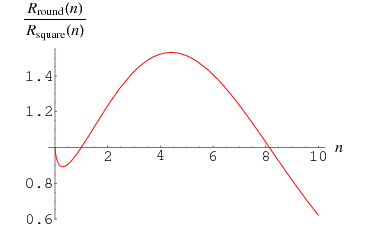
(Singmaster 1964). The ratio of these ratios is the transcendental equation

(6)

illustrated above, where the dimension 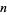 has been treated as a continuous quantity. This ratio crosses 1 at the value  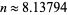(OEIS A127454), which must be determined numerically. As a result, a round peg fits better into a square hole than a square peg fits into a round hole only for integer dimensions .

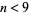REFERENCES:

Singmaster, D. "On Round Pegs in Square Holes and Square Pegs in Round Holes." Math. Mag. 37, 335-339, 1964.

Sloane, N. J. A. Sequence A127454 in "The On-Line Encyclopedia of Integer Sequences."

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 74, 1986.