
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-5-2020
Date: 3-3-2020
Date: 13-1-2020
|
The unitary divisor function 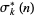 is the analog of the divisor function
is the analog of the divisor function 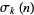 for unitary divisors and denotes the sum-of-
for unitary divisors and denotes the sum-of-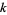 th-powers-of-the-unitary divisors function. As in the case of the usual divisor function,
th-powers-of-the-unitary divisors function. As in the case of the usual divisor function, 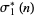 is commonly written
is commonly written 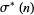 .
.
The numbers of unitary divisors 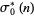 is the same as the numbers of squarefree divisors of
is the same as the numbers of squarefree divisors of 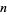 , as well as
, as well as 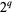 , where
, where 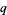 is the number of different primes dividing
is the number of different primes dividing 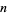 .
.
If 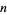 is squarefree, then
is squarefree, then 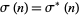 .
.
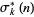 can be computed using the formula
can be computed using the formula
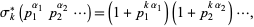 |
which can be computed in the Wolfram Language as
UnitaryDivisorSigma[k_, n_Integer] := Times @@
(1 + (Power @@@ FactorInteger[n])^k)
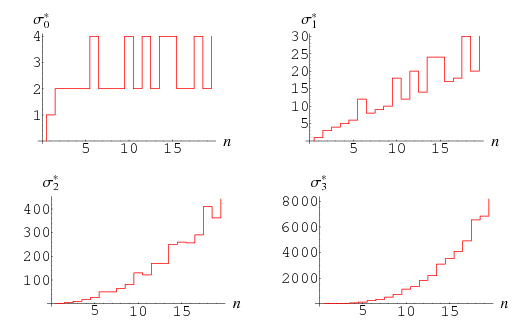
The following table gives 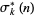 for
for 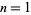 , 2, ... and small
, 2, ... and small 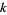 .
.
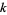 |
OEIS | 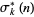 for for 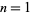 , 2, ... , 2, ... |
| 0 | A034444 | 1, 2, 2, 2, 2, 4, 2, 2, 2, 4, 2, 4, 2, 4, 4, 2, 2, 4, 2, 4, ... |
| 1 | A034448 | 1, 3, 4, 5, 6, 12, 8, 9, 10, 18, 12, 20, 14, 24, 24, ... |
| 2 | A034676 | 1, 5, 10, 17, 26, 50, 50, 65, 82, 130, 122, 170, 170, 250, 260, ... |
| 3 | A034677 | 1, 9, 28, 65, 126, 252, 344, 513, 730, 1134, 1332, 1820, ... |
| 4 | A034678 | 1, 17, 82, 257, 626, 1394, 2402, 4097, 6562, 10642, ... |
REFERENCES:
Sloane, N. J. A. Sequences A034444, A034448, A034676, A034677, and A034678 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|