Glaisher-Kinkelin Constant Digits

The decimal expansion of the Glaisher-Kinkelin constant is given by

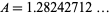(OEIS A074962). 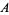 was computed to  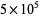decimal digits by E. Weisstein (Dec. 3, 2015).

The Earls sequence (starting position of 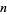 copies of the digit 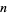) for 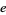 is given for 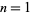, 2, ... by 7, 14, 2264, 1179, 411556, ... (OEIS A225763).

The digit sequences 0123456789 and 9876543210 do not occur in the first 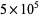 digits (E. Weisstein, Dec. 3, 2015).

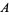-constant primes occur for 7, 10, 18, 64, 71, 527, 1992, 5644, 8813, 19692, ... (OEIS A118420) decimal digits.

The starting positions of the first occurrence of 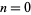, 1, 2, ... in the decimal expansion of  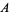(including the initial 1 and counting it as the first digit) are 12, 1, 2, 18, 5, 22, 14, 7, 3, 10, ... (OEIS A229193).

Scanning the decimal expansion of 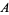 until all 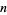-digit numbers have occurred, the last 1-, 2-, ... digit numbers appearing are 5, 98, 478, 9192, ... (OEIS A000000), which end at digits 22, 495, 7233, 100426, ... (OEIS A000000).

It is not known if the Glaisher-Kinkelin constant is normal in base 10, but the following table giving the counts of digits in the first 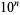 terms shows normal-appearing behavior up to at least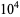 

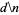	OEIS	10	100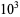
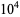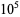0	A000000	0	11	96	999	9890
1	A000000	2	9	102	1033	9928
2	A000000	4	16	93	992	9977
3	A000000	0	8	100	1016	10055
4	A000000	1	8	99	955	10043
5	A000000	0	5	94	979	10034
6	A000000	0	12	96	988	10121
7	A000000	1	12	114	1067	9998
8	A000000	1	11	108	1031	9999
9	A000000	1	8	98	940	9955

REFERENCES:

Sloane, N. J. A. Sequences A074962, A118420, and A225763 in "The On-Line Encyclopedia of Integer Sequences."