Wolfram's Iteration

Wolfram's iteration is an algorithm for computing the square root of a rational number 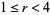 using properties of the binary representation of 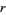. The algorithm begins with 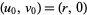, and then iterates

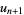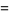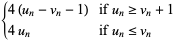			(1)
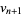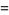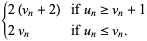			(2)

Interpreted as a binary number, 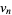 then converges to .

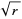For example, for 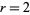 (i.e., Pythagoras's constant),  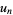is given by 2, 4, 16, 28, 28, 112, 92, 368, 28, ... (OEIS A095803), and  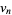by 0, 4, 8, 20, 44, 88, 180, 360, 724, ... (OEIS A095804). The binary representation of successive terms of  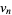(with the "binary" point shifted after the first term) are then

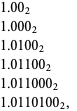(3)

as illustrated above, which can be seen to produce increasing numbers of digits in the binary representation of ,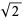

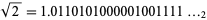(4)

(OEIS A004539). Interpreting the binary fractions produced at each step gives the sequence of approximations 1, 1, 5/4, 11/8, 11/8, 45/32, 45/32, 181/128, 181/128, ... (OEIS A095805 and A095806).

REFERENCES:

Sloane, N. J. A. Sequences A004539, OEIS A095803, OEIS A095804, OEIS A095805, and OEIS A095806 in "The On-Line Encyclopedia of Integer Sequences."

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 140-141 and 913, 2002.