


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-10-2018
Date: 5-9-2019
Date: 25-6-2019
|
There are two kinds of Bell polynomials.
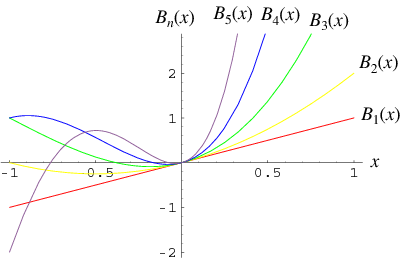
A Bell polynomial 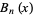 , also called an exponential polynomial and denoted
, also called an exponential polynomial and denoted 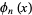 (Bell 1934, Roman 1984, pp. 63-67) is a polynomial
(Bell 1934, Roman 1984, pp. 63-67) is a polynomial  that generalizes the Bell number
that generalizes the Bell number 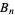 and complementary Bell number
and complementary Bell number 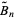 such that
such that
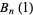 |
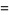 |
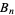 |
(1) |
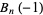 |
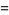 |
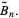 |
(2) |
These Bell polynomial generalize the exponential function.
Bell polynomials should not be confused with Bernoulli polynomials, which are also commonly denoted 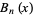 .
.
Bell polynomials are implemented in the Wolfram Language as BellB[n, x].
The first few Bell polynomials are
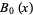 |
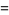 |
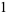 |
(3) |
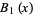 |
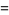 |
 |
(4) |
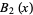 |
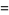 |
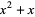 |
(5) |
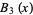 |
 |
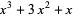 |
(6) |
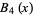 |
 |
 |
(7) |
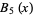 |
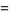 |
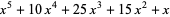 |
(8) |
 |
 |
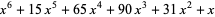 |
(9) |
(OEIS A106800).
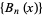 forms the associated Sheffer sequence for
forms the associated Sheffer sequence for
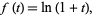 |
(10) |
so the polynomials have that exponential generating function
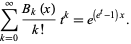 |
(11) |
Additional generating functions for 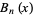 are given by
are given by
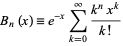 |
(12) |
or
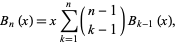 |
(13) |
with 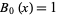 , where
, where 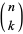 is a binomial coefficient.
is a binomial coefficient.
The Bell polynomials 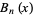 have the explicit formula
have the explicit formula
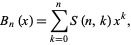 |
(14) |
where 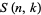 is a Stirling number of the second kind.
is a Stirling number of the second kind.
A beautiful binomial sum is given by
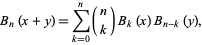 |
(15) |
where 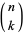 is a binomial coefficient.
is a binomial coefficient.
The derivative of 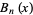 is given by
is given by
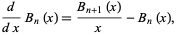 |
(16) |
so 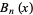 satisfies the recurrence equation
satisfies the recurrence equation
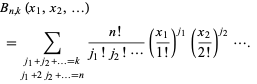 |
(17) |
The second kind of Bell polynomials 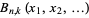 are defined by
are defined by
They have generating function
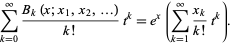 |
(18) |
REFERENCES:
Bell, E. T. "Exponential Polynomials." Ann. Math. 35, 258-277, 1934.
Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, p. 133, 1974.
Riordan, J. An Introduction to Combinatorial Analysis. New York: Wiley, pp. pp. 35-38, 49, and 142, 1980.
Roman, S. "The Exponential Polynomials" and "The Bell Polynomials." §4.1.3 and §4.1.8 in The Umbral Calculus. New York: Academic Press, pp. 63-67 and 82-87, 1984.
Sloane, N. J. A. Sequence A106800 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|