


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-3-2019
Date: 16-5-2018
Date: 9-6-2019
|
N. Nielsen (1909) and Ramanujan (Berndt 1985) considered the integrals
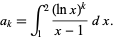 |
(1) |
They found the values for 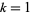 and 2. The general constants for
and 2. The general constants for 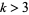 were found by Levin (1950) and, much later, independently by V. Adamchik (Finch 2003),
were found by Levin (1950) and, much later, independently by V. Adamchik (Finch 2003),
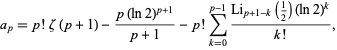 |
(2) |
where 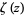 is the Riemann zeta function and
is the Riemann zeta function and 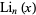 is the polylogarithm. The first few values are
is the polylogarithm. The first few values are
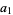 |
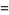 |
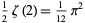 |
(3) |
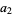 |
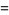 |
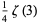 |
(4) |
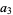 |
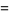 |
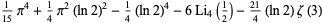 |
(5) |
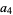 |
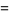 |
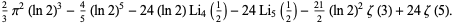 |
(6) |
REFERENCES:
Berndt, B. C. Ramanujan's Notebooks, Part I. New York: Springer-Verlag, 1985.
Borwein, J. M.; Bradley, D. M.; Broadhurst, D. J.; and Lisonek, P. "Special Values of Multidimensional Polylogarithms." Trans. Amer. Math. Soc. 353, 907-941, 2001.
Finch, S. R. "Apéry's Constant: Polylogarithms." §1.6.8 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 47-48, 2003.
Flajolet, P. and Salvy, B. "Euler Sums and Contour Integral Representation." Experim. Math. 7, 15-35, 1998.
Levin, V. I. "About a Problem of S. Ramanujan." Uspekhi Mat. Nauk 5, 161-166, 1950.
Nielsen, N. "Der Eulersche Dilogarithmus und seine Verallgemeinerungen." Nova Acta Leopoldina, Abh. der Kaiserlich Leopoldinisch-Carolinischen Deutschen Akad. der Naturforsch. 90, 121-212, 1909.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|