Inverse Hyperbolic Cosine

Min   Max       Re       Im

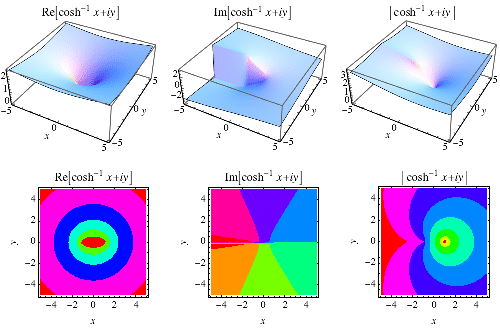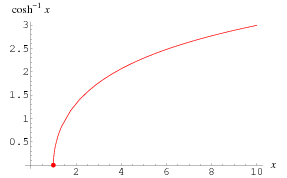
The inverse hyperbolic cosine 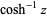 (Beyer 1987, p. 181; Zwillinger 1995, p. 481), sometimes called the area hyperbolic cosine (Harris and Stocker 1998, p. 264) is the multivalued function that is the inverse function of the hyperbolic cosine.

The variants 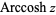 and 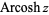 (Harris and Stocker 1998, p. 263) are sometimes used to refer to explicit principal values of the inverse cotangent, although this distinction is not always made. Worse yet, the notation  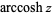is sometimes used for the principal value, with  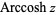being used for the multivalued function (Abramowitz and Stegun 1972, p. 87). The function is sometimes denoted  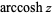(Abramowitz and Stegun 1972, p. 87; Jeffrey 2000, p. 124) or  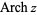(Gradshteyn and Ryzhik 2000, p. xxx). Note that in the notation 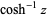, 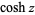is the hyperbolic cosine and the superscript  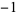denotes an inverse function, not the multiplicative inverse.

The principal value of 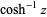 is implemented in the Wolfram Language as ArcCosh[z], and in the GNU C library as acosh(double x).

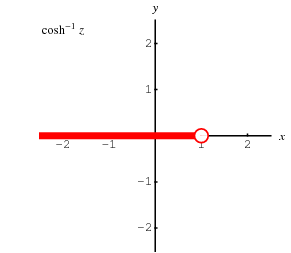
The inverse hyperbolic cosine is a multivalued function and hence requires a branch cut in the complex plane, which the Wolfram Language's convention places at the line segment 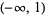. This follows from the definition of  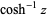as

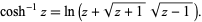(1)

Gradshteyn and Ryzhik (2000, p. xxx) give a version of the inverse hyperbolic cosine which holds only in the upper half of the complex plane  and for 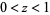. The corresponding corrected formulas are

(2)

which can be written in general form as

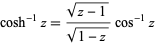(3)

(Wolfram Functions Site).

The derivative of the inverse hyperbolic cosine is

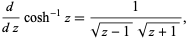(4)

and its indefinite integral is

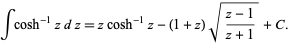(5)

For real 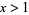, it satisfies

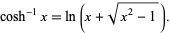(6)

The inverse hyperbolic cosine has the Maclaurin series,

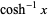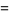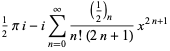			(7)
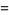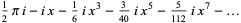			(8)

(OEIS A055786 and A002595), where 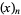 is a Pochhammer symbol.

Puiseux series

(9)

(OEIS A055786 and A091019) about 1, and the Taylor series

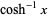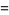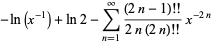			(10)
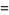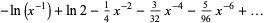			(11)

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Inverse Hyperbolic Functions." §4.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 86-89, 1972.

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 142-143, 1987.

GNU C Library. "Mathematics: Inverse Trigonometric Functions." http://www.gnu.org/manual/glibc-2.2.3/html_chapter/libc_19.html#SEC391.

Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. xxx, 2000.

Harris, J. W. and Stocker, H. Handbook of Mathematics and Computational Science. New York: Springer-Verlag, 1998.

Jeffrey, A. "Inverse Trigonometric and Hyperbolic Functions." §2.7 in Handbook of Mathematical Formulas and Integrals, 2nd ed.Orlando, FL: Academic Press, pp. 124-128, 2000.

Sloane, N. J. A. Sequences A002595/M4233, A052468, A052469, A055786 and A091019 in "The On-Line Encyclopedia of Integer Sequences."

Spanier, J. and Oldham, K. B. "Inverse Trigonometric Functions." Ch. 35 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 331-341, 1987.

Wolfram Functions Site. "ArcCosh." http://functions.wolfram.com/ElementaryFunctions/ArcCosh/27/02/03/01/01/.

Zwillinger, D. (Ed.). "Inverse Hyperbolic Functions." §6.8 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 481-483, 1995.