


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-8-2018
Date: 14-10-2019
Date: 16-4-2019
|
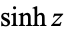 ,
, 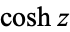 ,
, 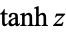 ,
, 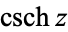 ,
, 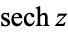 ,
, 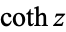 (hyperbolic sine, hyperbolic cosine, hyperbolic tangent, hyperbolic cosecant, hyperbolic secant, and hyperbolic cotangent) are analogs of the circular functions, defined by removing
(hyperbolic sine, hyperbolic cosine, hyperbolic tangent, hyperbolic cosecant, hyperbolic secant, and hyperbolic cotangent) are analogs of the circular functions, defined by removing 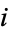 s appearing in the complex exponentials. For example,
s appearing in the complex exponentials. For example,
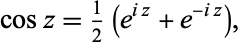 |
(1) |
so
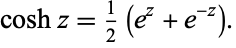 |
(2) |
Note that alternate notations are sometimes used, as summarized in the following table.
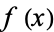 |
alternate notations |
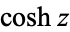 |
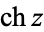 (Gradshteyn and Ryzhik 2000, p. xxvii) (Gradshteyn and Ryzhik 2000, p. xxvii) |
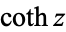 |
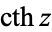 (Gradshteyn and Ryzhik 2000, p. xxvii) (Gradshteyn and Ryzhik 2000, p. xxvii) |
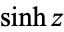 |
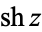 (Gradshteyn and Ryzhik 2000, p. xxvii) (Gradshteyn and Ryzhik 2000, p. xxvii) |
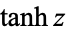 |
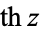 (Gradshteyn and Ryzhik 2000, p. xxvii) (Gradshteyn and Ryzhik 2000, p. xxvii) |
The hyperbolic functions share many properties with the corresponding circular functions. In fact, just as the circle can be represented parametrically by
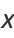 |
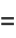 |
 |
(3) |
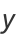 |
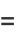 |
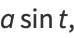 |
(4) |
a rectangular hyperbola (or, more specifically, its right branch) can be analogously represented by
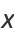 |
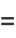 |
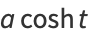 |
(5) |
 |
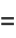 |
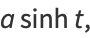 |
(6) |
where 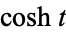 is the hyperbolic cosine and
is the hyperbolic cosine and 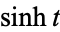 is the hyperbolic sine.
is the hyperbolic sine.
The hyperbolic functions arise in many problems of mathematics and mathematical physics in which integrals involving 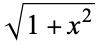 arise (whereas the circular functions involve
arise (whereas the circular functions involve 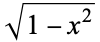 ). For instance, the hyperbolic sine arises in the gravitational potential of a cylinder and the calculation of the Roche limit. The hyperbolic cosine function is the shape of a hanging cable (the so-called catenary). The hyperbolic tangent arises in the calculation of and rapidity of special relativity. All three appear in the Schwarzschild metric using external isotropic Kruskal coordinates in general relativity. The hyperbolic secant arises in the profile of a laminar jet. The hyperbolic cotangent arises in the Langevin function for magnetic polarization.
). For instance, the hyperbolic sine arises in the gravitational potential of a cylinder and the calculation of the Roche limit. The hyperbolic cosine function is the shape of a hanging cable (the so-called catenary). The hyperbolic tangent arises in the calculation of and rapidity of special relativity. All three appear in the Schwarzschild metric using external isotropic Kruskal coordinates in general relativity. The hyperbolic secant arises in the profile of a laminar jet. The hyperbolic cotangent arises in the Langevin function for magnetic polarization.
The hyperbolic functions are defined by
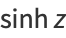 |
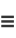 |
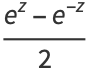 |
(7) |
 |
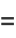 |
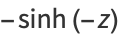 |
(8) |
 |
 |
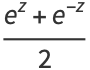 |
(9) |
 |
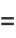 |
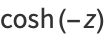 |
(10) |
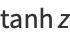 |
 |
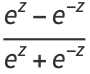 |
(11) |
 |
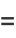 |
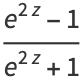 |
(12) |
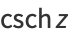 |
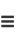 |
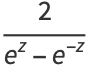 |
(13) |
 |
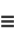 |
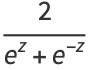 |
(14) |
 |
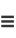 |
 |
(15) |
 |
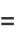 |
 |
(16) |
For arguments multiplied by 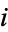 ,
,
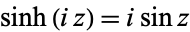 |
(17) |
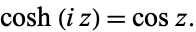 |
(18) |
The hyperbolic functions satisfy many identities analogous to the trigonometric identities (which can be inferred using Osborn's rule) such as
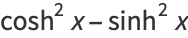 |
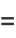 |
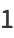 |
(19) |
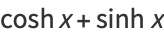 |
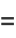 |
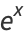 |
(20) |
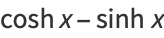 |
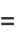 |
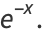 |
(21) |
See also Beyer (1987, p. 168).
Some half-angle formulas are
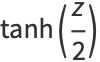 |
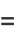 |
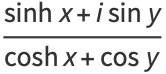 |
(22) |
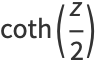 |
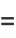 |
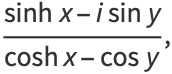 |
(23) |
where 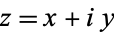 .
.
Some double-angle formulas are
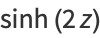 |
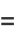 |
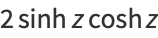 |
(24) |
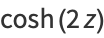 |
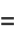 |
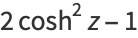 |
(25) |
 |
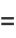 |
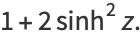 |
(26) |
Identities for complex arguments include
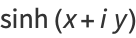 |
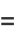 |
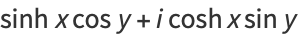 |
(27) |
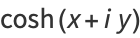 |
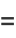 |
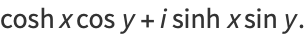 |
(28) |
The absolute squares for complex arguments are
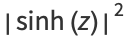 |
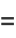 |
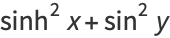 |
(29) |
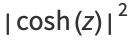 |
 |
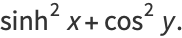 |
(30) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Hyperbolic Functions." §4.5 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 83-86, 1972.
Anderson, J. W. "Trigonometry in the Hyperbolic Plane." §5.7 in Hyperbolic Geometry. New York: Springer-Verlag, pp. 146-151, 1999.
Beyer, W. H. "Hyperbolic Function." CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 168-186 and 219, 1987.
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 126-131, 1967.
Harris, J. W. and Stocker, H. "Hyperbolic Functions." Handbook of Mathematics and Computational Science. New York: Springer-Verlag, pp. 245-262, 1998.
Jeffrey, A. "Hyperbolic Identities." §2.5 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 117-122, 2000.
Yates, R. C. "Hyperbolic Functions." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 113-118, 1952.
Zwillinger, D. (Ed.). "Hyperbolic Functions." §6.7 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 476-481 1995.



|
|
|
|
صحة الفم في خطر.. 5 أخطاء شائعة أثناء تنظيف الأسنان
|
|
|
|
|
|
|
نقلة نوعية في مراقبة السكري.. جهاز جديد لقياس السكر في الدم دون وخز
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|