المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Power Polynomial |
 783
 10:44 صباحاً
date: 17-2-2019 |
Author : Roman, S 
Book or Source : "The Sequence x^n." §4.1.1 in The Umbral Calculus. New York: Academic Press, 
Page and Part : p. 55|
Read More
Date: 11-3-2019
1379
Date: 19-1-2019
1075
Date: 4-3-2019
1550
|
The power polynomials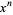 
are an associated Sheffer sequence with
 |
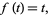(1) |
giving generating function
 |
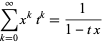(2) |
and exponential generating function
 |
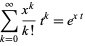(3) |
and binomial identity
 |
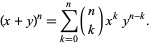(4) |
REFERENCES:
Roman, S. "The Sequence 
." §4.1.1 in The Umbral Calculus. New York: Academic Press, p. 55, 1984.
|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|
