


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-3-2017
Date: 13-2-2019
Date: 21-1-2019
|
For a polynomial
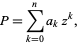 |
(1) |
several classes of norms are commonly defined. The 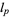 -norm is defined as
-norm is defined as
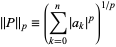 |
(2) |
for 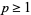 , giving the special cases
, giving the special cases
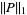 |
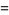 |
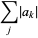 |
(3) |
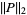 |
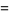 |
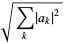 |
(4) |
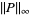 |
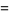 |
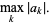 |
(5) |
Here, 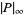 is called the polynomial height. Note that some authors (especially in the area of Diophantine analysis) use
is called the polynomial height. Note that some authors (especially in the area of Diophantine analysis) use 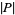 as a shorthand for
as a shorthand for 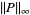 and
and 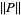 as a shorthand for
as a shorthand for 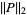 , while others (especially in the area of computational complexity) used
, while others (especially in the area of computational complexity) used 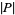 to denote the
to denote the 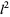 -norm
-norm 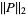 and (Zippel 1993, p. 174).
and (Zippel 1993, p. 174).
Another class of norms is the 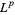 -norms, defined by
-norms, defined by
![||P||_(L_p)=[int_0^(2pi)|P(e^(itheta))|^p(dtheta)/(2pi)]^(1/p)](http://mathworld.wolfram.com/images/equations/PolynomialNorm/NumberedEquation3.gif) |
(6) |
for 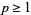 , giving the special cases
, giving the special cases
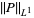 |
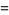 |
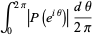 |
(7) |
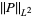 |
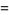 |
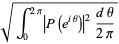 |
(8) |
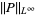 |
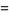 |
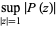 |
(9) |
(Borwein and Erdélyi 1995, p. 6).
REFERENCES:
Borwein, P. and Erdélyi, T. "Norms on 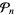 ." §1.1.E.3 in Polynomials and Polynomial Inequalities. New York: Springer-Verlag, pp. 6-7, 1995.
." §1.1.E.3 in Polynomials and Polynomial Inequalities. New York: Springer-Verlag, pp. 6-7, 1995.
Zippel, R. Effective Polynomial Computation. Boston, MA: Kluwer, 1993.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|