


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-2-2019
Date: 4-3-2019
Date: 23-2-2019
|
Given a field 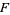 and an extension field
and an extension field 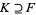 , an element
, an element 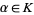 is called algebraic over
is called algebraic over 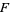 if it is a root of some nonzero polynomial with coefficients in
if it is a root of some nonzero polynomial with coefficients in 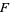 .
.
Obviously, every element of 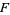 is algebraic over
is algebraic over 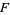 . Moreover, the sum, difference, product, and quotient of algebraic elements are again algebraic. It follows that the simple extension field
. Moreover, the sum, difference, product, and quotient of algebraic elements are again algebraic. It follows that the simple extension field 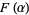 is an algebraic extension of
is an algebraic extension of 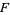 iff
iff 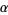 is algebraic over
is algebraic over 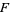 .
.
The imaginary unit i is algebraic over the field 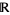 of real numbers since it is a root of the polynomial
of real numbers since it is a root of the polynomial 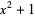 . Because its coefficients are integers, it is even true that
. Because its coefficients are integers, it is even true that 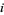 is algebraic over the field
is algebraic over the field 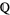 of rational numbers, i.e., it is an algebraic number (and also an algebraic integer). As a consequence,
of rational numbers, i.e., it is an algebraic number (and also an algebraic integer). As a consequence, 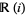 and
and 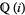 are algebraic extensions of
are algebraic extensions of 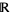 and
and 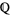 respectively. (Here,
respectively. (Here, 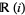 is the complex field
is the complex field 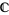 , whereas
, whereas 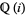 is the total ring of fractions of the ring of Gaussian integers
is the total ring of fractions of the ring of Gaussian integers ![Z[i]](http://mathworld.wolfram.com/images/equations/AlgebraicElement/Inline23.gif) .)
.)



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|