


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-10-2018
Date: 18-10-2018
Date: 18-10-2018
|
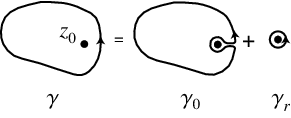
Cauchy's integral formula states that
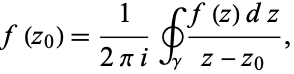 |
(1) |
where the integral is a contour integral along the contour 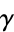 enclosing the point
enclosing the point 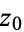 .
.
It can be derived by considering the contour integral
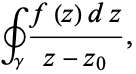 |
(2) |
defining a path 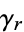 as an infinitesimal counterclockwise circle around the point
as an infinitesimal counterclockwise circle around the point 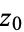 , and defining the path
, and defining the path 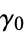 as an arbitrary loop with a cut line (on which the forward and reverse contributions cancel each other out) so as to go around
as an arbitrary loop with a cut line (on which the forward and reverse contributions cancel each other out) so as to go around 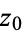 . The total path is then
. The total path is then
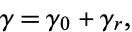 |
(3) |
so
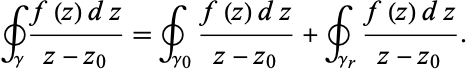 |
(4) |
From the Cauchy integral theorem, the contour integral along any path not enclosing a pole is 0. Therefore, the first term in the above equation is 0 since 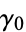 does not enclose the pole, and we are left with
does not enclose the pole, and we are left with
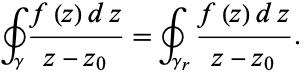 |
(5) |
Now, let 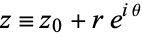 , so
, so 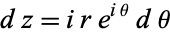 . Then
. Then
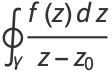 |
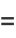 |
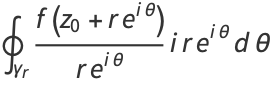 |
(6) |
 |
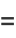 |
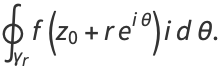 |
(7) |
But we are free to allow the radius 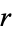 to shrink to 0, so
to shrink to 0, so
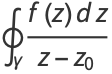 |
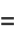 |
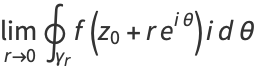 |
(8) |
 |
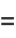 |
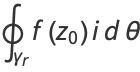 |
(9) |
 |
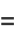 |
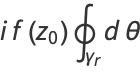 |
(10) |
 |
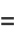 |
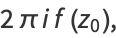 |
(11) |
giving (1).
If multiple loops are made around the point 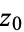 , then equation (11) becomes
, then equation (11) becomes
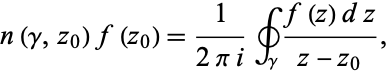 |
(12) |
where 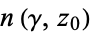 is the contour winding number.
is the contour winding number.
A similar formula holds for the derivatives of 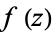 ,
,
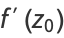 |
 |
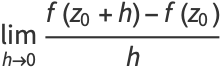 |
(13) |
 |
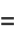 |
![lim_(h->0)1/(2piih)[∮_gamma(f(z)dz)/(z-z_0-h)-∮_gamma(f(z)dz)/(z-z_0)]](http://mathworld.wolfram.com/images/equations/CauchyIntegralFormula/Inline37.gif) |
(14) |
 |
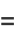 |
![lim_(h->0)1/(2piih)∮_gamma(f(z)[(z-z_0)-(z-z_0-h)]dz)/((z-z_0-h)(z-z_0))](http://mathworld.wolfram.com/images/equations/CauchyIntegralFormula/Inline40.gif) |
(15) |
 |
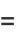 |
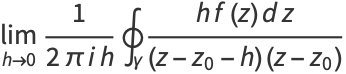 |
(16) |
 |
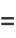 |
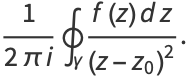 |
(17) |
Iterating again,
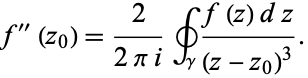 |
(18) |
Continuing the process and adding the contour winding number 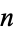 ,
,
 |
(19) |
REFERENCES:
Arfken, G. "Cauchy's Integral Formula." §6.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 371-376, 1985.
Kaplan, W. "Cauchy's Integral Formula." §9.9 in Advanced Calculus, 4th ed. Reading, MA: Addison-Wesley, pp. 598-599, 1991.
Knopp, K. "Cauchy's Integral Formulas." Ch. 5 in Theory of Functions Parts I and II, Two Volumes Bound as One, Part I. New York: Dover, pp. 61-66, 1996.
Krantz, S. G. "The Cauchy Integral Theorem and Formula." §2.3 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 26-29, 1999.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 367-372, 1953.
Woods, F. S. "Cauchy's Theorem." §146 in Advanced Calculus: A Course Arranged with Special Reference to the Needs of Students of Applied Mathematics. Boston, MA: Ginn, pp. 352-353, 1926.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|