
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-10-2018
Date: 28-11-2018
Date: 24-10-2018
|
 |
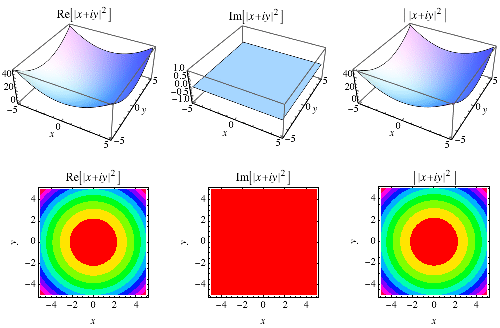 |
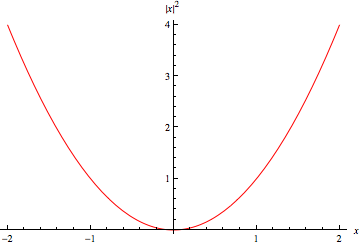
The absolute square of a complex number 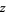 , also known as the squared norm, is defined as
, also known as the squared norm, is defined as
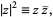 |
(1) |
where 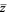 denotes the complex conjugate of
denotes the complex conjugate of 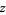 and
and 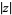 is the complex modulus.
is the complex modulus.
If the complex number is written 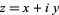 , with
, with  and
and 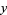 real, then the absolute square can be written
real, then the absolute square can be written
 |
(2) |
If 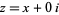 is a real number, then (1) simplifies to
is a real number, then (1) simplifies to
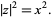 |
(3) |
An absolute square can be computed in terms of  and
and 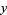 using the Wolfram Language command ComplexExpand[Abs[z]^2, TargetFunctions ->
using the Wolfram Language command ComplexExpand[Abs[z]^2, TargetFunctions -> 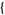 Conjugate
Conjugate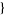 ].
].
An important identity involving the absolute square is given by
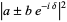 |
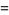 |
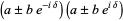 |
(4) |
 |
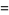 |
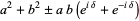 |
(5) |
 |
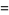 |
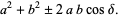 |
(6) |
If 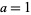 , then (6) becomes
, then (6) becomes
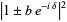 |
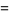 |
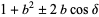 |
(7) |
 |
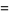 |
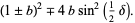 |
(8) |
If 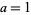 , and
, and 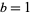 , then
, then
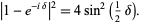 |
(9) |
Finally,
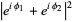 |
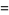 |
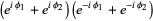 |
(10) |
 |
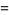 |
![2[1+cos(phi_2-phi_1)]](http://mathworld.wolfram.com/images/equations/AbsoluteSquare/Inline36.gif) |
(11) |
 |
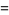 |
![4cos^2[1/2(phi_2-phi_1)].](http://mathworld.wolfram.com/images/equations/AbsoluteSquare/Inline39.gif) |



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|