


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-8-2019
Date: 25-4-2019
Date: 25-5-2019
|
The fractional derivative of 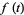 of order
of order 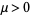 (if it exists) can be defined in terms of the fractional integral
(if it exists) can be defined in terms of the fractional integral 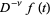 as
as
![D^muf(t)=D^m[D^(-(m-mu))f(t)],](http://mathworld.wolfram.com/images/equations/FractionalDerivative/NumberedEquation1.gif) |
(1) |
where 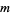 is an integer
is an integer ![>=[mu]](http://mathworld.wolfram.com/images/equations/FractionalDerivative/Inline5.gif) , where
, where ![[x]](http://mathworld.wolfram.com/images/equations/FractionalDerivative/Inline6.gif) is the ceiling function. The semiderivative corresponds to
is the ceiling function. The semiderivative corresponds to 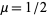 .
.
The fractional derivative of the function 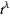 is given by
is given by
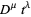 |
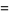 |
![D^m[D^(-(m-mu))t^lambda]](http://mathworld.wolfram.com/images/equations/FractionalDerivative/Inline11.gif) |
(2) |
 |
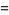 |
![D^m[(Gamma(lambda+1))/(Gamma(lambda+m-mu+1))t^(lambda+m-mu)]](http://mathworld.wolfram.com/images/equations/FractionalDerivative/Inline14.gif) |
(3) |
 |
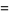 |
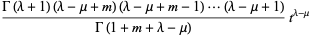 |
(4) |
 |
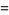 |
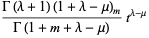 |
(5) |
 |
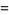 |
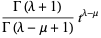 |
(6) |
for 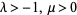 . The fractional derivative of the constant function
. The fractional derivative of the constant function 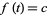 is then given by
is then given by
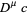 |
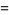 |
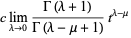 |
(7) |
 |
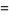 |
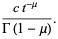 |
(8) |
The fractional derivate of the Et-function is given by
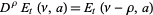 |
(9) |
for 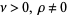 .
.
It is always true that, for 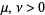 ,
,
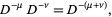 |
(10) |
but not always true that
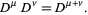 |
(11) |
A fractional integral can also be similarly defined. The study of fractional derivatives and integrals is called fractional calculus.
REFERENCES:
Kilbas, A. A.; Srivastava, H. M.; and Trujiilo, J. J. Theory and Applications of Fractional Differential Equations. Amsterdam, Netherlands: Elsevier, 2006.
Love, E. R. "Fractional Derivatives of Imaginary Order." J. London Math. Soc. 3, 241-259, 1971.
Miller, K. S. "Derivatives of Noninteger Order." Math. Mag. 68, 183-192, 1995.
Oldham, K. B. and Spanier, J. The Fractional Calculus: Integrations and Differentiations of Arbitrary Order. New York: Academic Press, 1974.
Samko, S. G.; Kilbas, A. A.; and Marichev, O. I. Fractional Integrals and Derivatives. Yverdon, Switzerland: Gordon and Breach, 1993.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|