تحويل الموجات الكهرومغناطيسية
المؤلف:
د. حسون. ناظم احمد ، د. شاحوت. عياد مفتاح و د. ابراهيم. بثينة عبد المنعم
المصدر:
النظرية النسبية الخاصة
الجزء والصفحة:
ص150
26-4-2016
4301
تحويل الموجات الكهرومغناطيسية
ان الزخم الاعتيادي في الفضاء ذي الابعاد الثلاثة 
والطاقة الكلية ε لجسيم يمكن توحيدهما ليكونا متجها رباعيا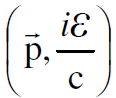 
ووفقا لفكرة تكميم الطاقة لبلانك فان الفوتون وتحت ظروف معينة* يسلك سلوك الجسيم ولقد بينا كيف يكون لهذا الفوتون زخم مساو الى :
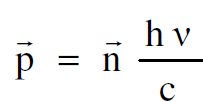
وطاقة مساوية الى :
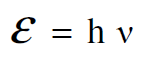
حيث ان v التردد، h ثابت بلانك و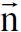 
وحدة المتجه باتجاه حركة الفوتون.
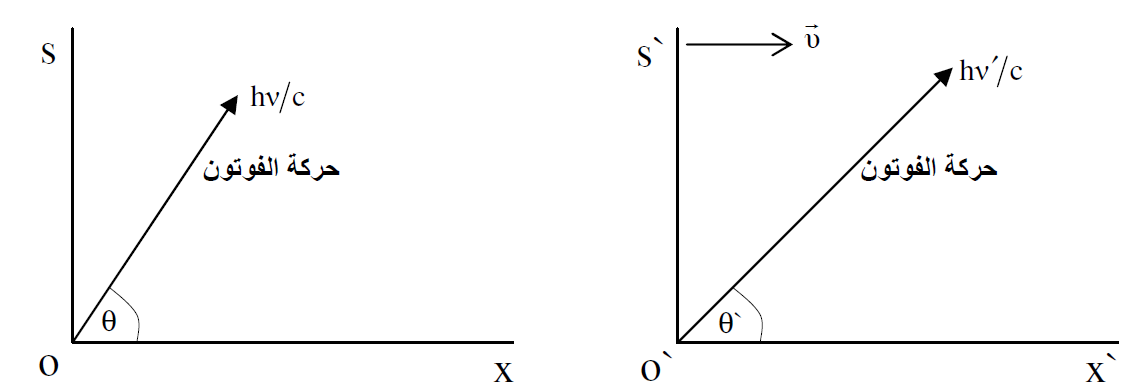
الشكل (1.1) : فوتون يتحرك باتجاه يصنع زاوية θ مع x في s. يتغير زمن الفوتون في sʹ ويصنع زاوية ʹθ مع xʹ.
وبالنسبة للفوتون يمكننا كتابة المتجه الرباعي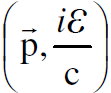 
بالشكل 
.
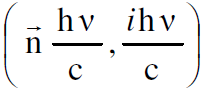لنفرض الان فوتونا منفردا يتحرك في المستوى x-y في محور الاسناد s وفي المستوى ʹxʹ-y في محور الاسناد sʹ بحيث يصنع اتجاه حركته الزاويتين θʹ, θ مع الاحداثيين xʹ, x لمحوري الاسناد sʹ, s على التوالي كما في الشكل (1.1). واذا كان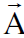 
متجها رباعيا فان :
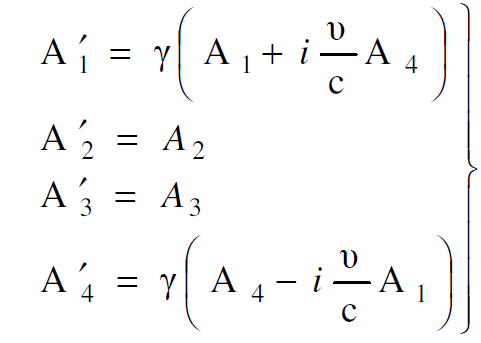(1.1)
وبتطبيق هذه المعادلات على الزخم الرباعي للفوتون نحصل على :
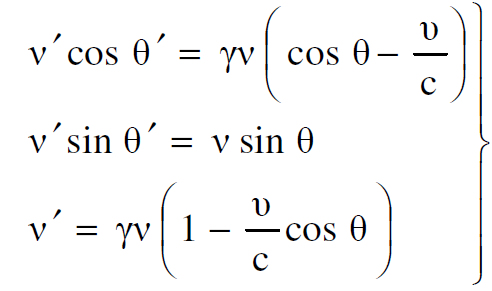(1.2)
اذا اعتبرنا الان ان الضوء موجة كهرومغناطيسية تسير بالسرعة c في الفراغ وهي واحدة بالنسبة لجميع محاور الاسناد واعتبرنا v تردد هذه الموجة في محور الاسناد s اتجاهها يصنع زاوية مقدارها θ مع الاحداثي x وان ʹv ترددها في محور الاسناد sʹ واتجاهها يصنع ʹθ مع الاحداثي xʹ لامكننا ان نثبت بان المعادلات أعلاه التي توصلنا اليها بمساعدة المتجهات الرباعية هي معادلات تحويل الموجة المستوية من محور الاسناد s الى محور الاسناد sʹ وتبين معادلات التحويل هذه كيف ان اتجاه انتشار الموجة المستوية والتردد قد تم توحيدها ليكونا متجها رباعيا هو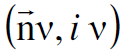 
حيث ان 
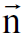وحدة المتجه باتجاه انتشار الموجة المستوية وان v ترددها. لاحظ الشكل (1.2).
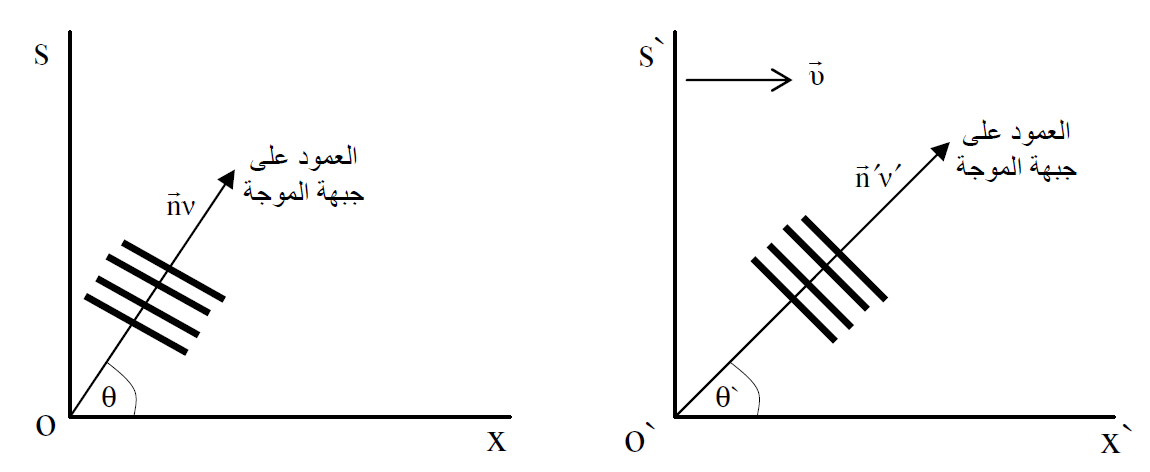
الشكل (1.2) : موجة كهرومغناطيسية مستوية يصنع العمد على جهتها زاوية θ في s. ويصنع العمود على جبهتها في sʹ الزاوية ʹθ.
اذا ضربنا الان بالمقدار h/c يتحول المتجه الرباعي للموجة المستوية الى الصيغة التالية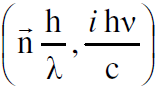 
وهكذا نلاحظ بالنسبة للضوء ان الزخم والطاقة العائدين للفوتون يمكن توحيدهما ليكونا المتجه الرباعي 
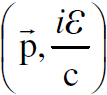كما أن الطول الموجي وتردد الموجة المستوية يمكن توحيدهما ليكونا متجها رباعيا بالصيغة 
.
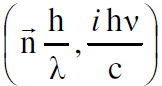لقد اقترح العالم الفرنسي لويس ديبرولي سنة 1923، (أي بعد اكثر من عقدين من الزمن على ظهور فكرة تكميم الطاقة لبلانك) انه اذا كان الاشعاع تحت بعض الظروف قد يسلك سلوكا مزدوجا، فانه من الممكن افتراض ان المادة قد تسلك أيضا سلوكا مزدوجا في ظروف اخرى. لقد افترض ديبرولي ان الجسيمات المادية (الإلكترونات) تصبحها موجة (تعرف الان بموجة ديبرولي) وان طول هذه الموجة الموافقة يتناسب مع الزخم بصورة مشابهة للفوتون. فان صحت هذه الفرضية، فان مقارنة مع الضوء نتوقع ان يتحد الزخم مع الطاقة ليكونا المتجه الرباعي للجسيم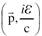 
فيما يتحد الطول الموجي والتردد العائدين لموجة الجسيم، كما هو متوقع، ليكونا المتجه الرباعي للموجة 
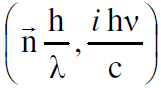، حيث ان 
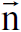وحدة المتجه باتجاه انتشار الموجة المرافقة للجسيم.
اقترح ديبرولي كذلك بانه قد تكون علاقة بلانك ε = h v صحيحة ويمكن تطبيقها على الجسيمات، حيث v هنا تردد الموجة المرافقة للجسيم وفي هذه الحالة يمكن ان يكتب المتجه الرباعي للموجة المرافقة بالصيغة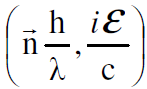 
وبمقارنة المتجه الرباعي 
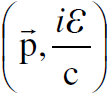يمكننا ان نتوقع ايضا بان الزخم يساوي
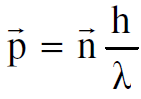
او
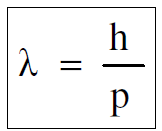
وهي علاقة ديبرولي التي أثبتت تجريبيا بعد اربع سنوات من اقتراحها، حيث قام العالمان دافيسون وجيرمر سنة 1927 بمشاهدة حيود الالكترونات عند سقوطها على سطح بلورة من النيكل والتي بينا فيها ان الدليل القاطع على وجود الامواج المصاحبة للإلكترونات هو تحقيقها العملي لظاهرة الحيود.
- سرعة الطور vph لموجات ديبرولي تساوي :
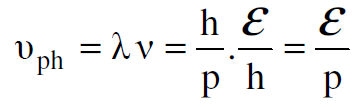
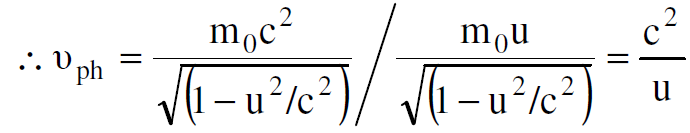(1.3)
- سرعة مجموعة الامواج vg فهي تساوي :
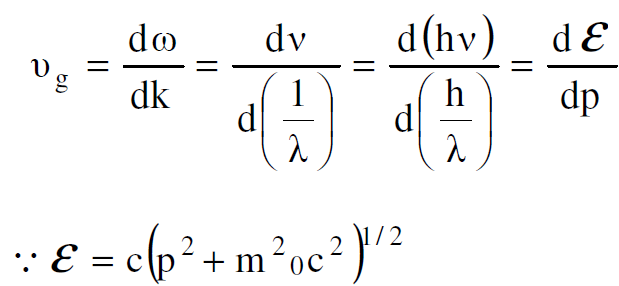
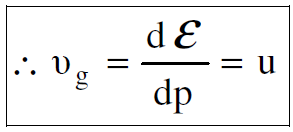(1.4)
اذن سرعة المجموعة vg لموجات ديبرولي تساوي سرعة الجسيم u. لذلك فان فكرة تمثيل الجسيم المادي بموجة مرافقة (أو مجموعة من الامواج) تسير بسرعته نفسها وتحمل صفاته نفسها تبدو مقبولة علميا.
ــــــــــــــــــــــــــــــــــــــــــ
* وفقا لفرضية اينشتاين يمتلك الفوتون صفات الازدواجية الموجبة الجسيمية عند الانتشار والحيود والتداخل، فتظهر صفاته الموجبة وتختفي الجسيمية. اما عند تفاعل الفوتون مع المادة كما هو الحال في الظاهرة الكهروضوئية وتأثير كمبتون فتظهر صفاته الجسيمية وتختفي الموجة.
الاكثر قراءة في النظرية النسبية الخاصة
اخر الاخبار
اخبار العتبة العباسية المقدسة
