Mathematical Derivation

To determine the density of allowed quantum states as a function of energy, we need to consider an appropriate mathematical model. Electrons are allowed to move relatively freely in the conduction band of a semiconductor, but are confined to the crystal. As a first step, we will consider a free electron confined to a three-dimensional infinite potential well, where the potential well represents the crystal. The potential of the infinite potential well is defined as

(1)

where the crystal is assumed to be a cube with length a. Schrodinger's wave equation in three dimensions can be solved using the separation of variables technique. Extrapolating the results from the one-dimensional infinite potential well, we can show that

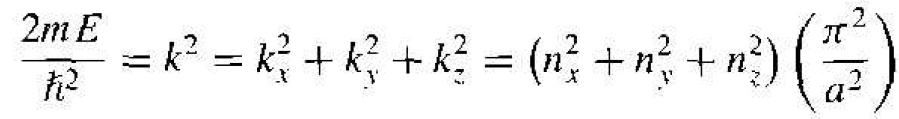(2)

where n_x, n_y, and n_z are positive integers. (Negative values of n_x, n_y,  and n_z yield the same wave function, except for the sign, as the positive integer values, resulting in the same probability function and energy, so the negative integers do not represent a different quantum state.)

We can schematically plot the allowed quantum states in k space. Figure 1.1a shows a two-dimensional plot as a function of k_x and k_y. Each point represents an allowed quantum state corresponding to various integral values of n_x and n_y. Positive and negative values of k_x, k_y, or k_z have the same energy and represent the same

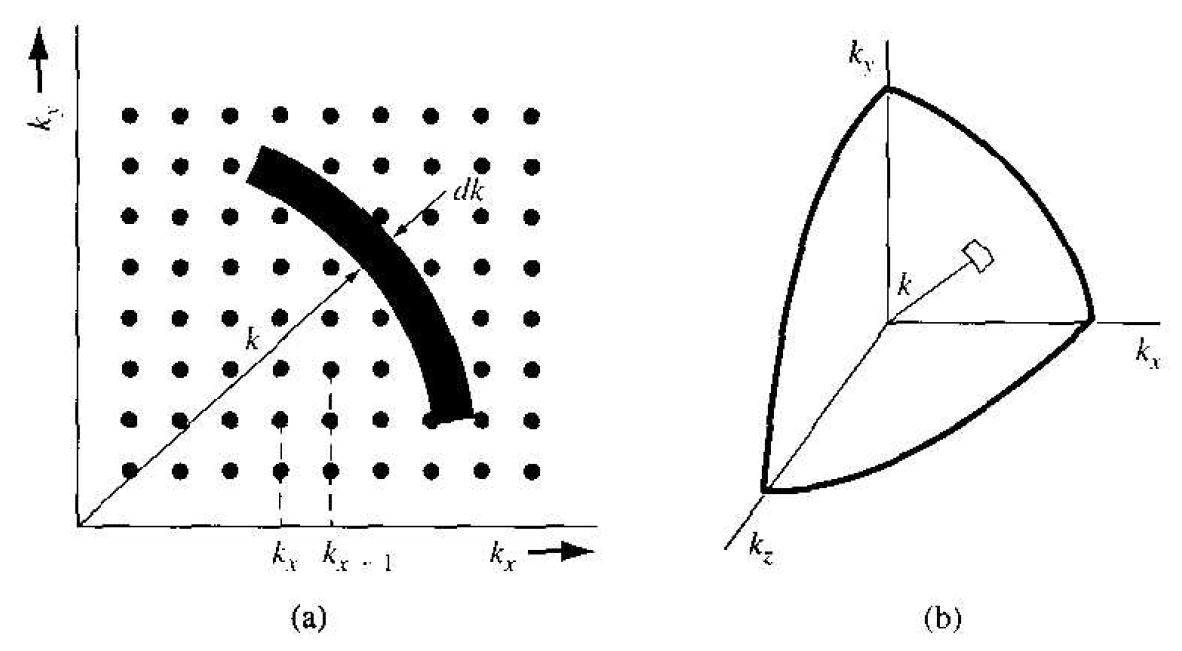
Figure 1.1 (a) A two-dimensional army of allowed quantum stales in k space. (b) The positive one-eighth of the spherical k space.

energy state. Since negative values of k_x, k_y, or k_z do not represent additional quantum states, the density of quantum states will be determined by considering only the positive one-eighth of the spherical k space as shown in Figure 1.1b.

The distance between two quantum states in the k_x direction, for example, is given by

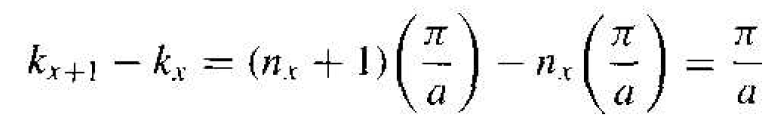(3)

Generalizing this result to three dimensions, the volume V_k of a single quantum state is

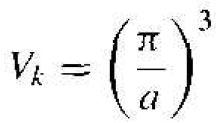(4)

We can now determine the density of quantum states in k space. A differential volume in k space is shown in Figure 1.1b and is given by 4πk² dk, so the differential density of quantum states in k space can he written as

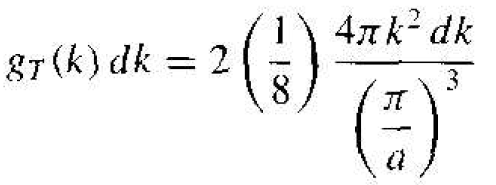(5)

The first factor, 2, takes into account the two spin states allowed for each quantum stale; the next factor, 1/8, takes into account that we are considering only the quantum states for positive values of k_x, k_y, and k_z. The factor 4πk² dk, is again the differential volume and the factor (π/a)³ is the volume of one quantum state. Equation (5) may be simplified to

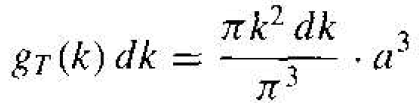(6)

Equation (6) gives the density of quantum states as a function of momentum, through the parameter k. We can now determine the density of quantum states as a function of energy E. For a free electron, the parameters E and k are related by

(7a)

or

(7b)

The differential dk is

(8)

Then, substituting the expressions for k² and dk into Equation (6). the number of energy states between E and E + dE is given by

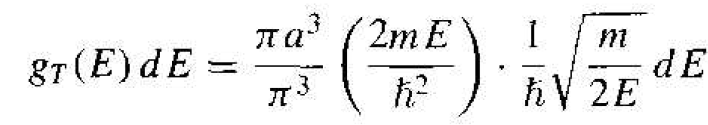(9)

Since h = h/2π, Equation (9) becomes

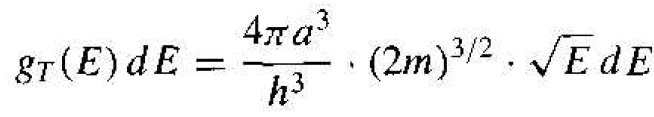(10)

Equation (10) gives the total number of quantum states between the energy E and E + dE in the crystal space volume of a³. If we divide by the volume a³, then we will obtain the density of quantum states per unit volume of the crystal. Equation (10) then becomes

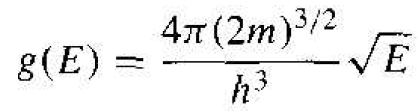(11)

The density of quantum states is a function of energy E. As the energy of this free electron becomes small, the number of available quantum states decreases. This density function is really a double density, in that the units are given in terms of states per unit energy per unit volume.