


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 28-7-2016
Date: 14-8-2016
Date: 9-8-2016
|
Teacup Engine
was peacefully drinking tea at five o’clock galactic time, as was his wont, when he had an emergency outside the shuttle, and he had to do an EVA to deal with it. Upon leaving the ship, his jetpack failed, and nothing remained to connect him to the shuttle. Fortunately, he had absentmindedly brought his teacup with him. Since this was the only cup he had, he did not want to throw it away in order to propel him back to the shuttle (besides, it was his favorite cup). Instead, he used the sublimation of the frozen tea to propel him back to the spaceship (see Figure 1.1). Was it really possible? Estimate the time it might take him to return if he is a distance L = 40 m from the ship. Assume that the sublimation occurs at a constant temperature T = 273 K.
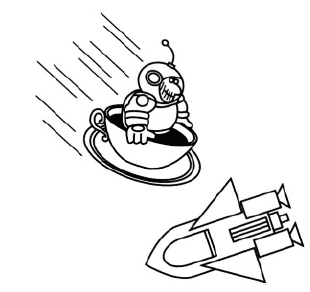
Figure 1.1
The vapor pressure at this temperature is P0 = 600Pa, and the total mass of the astronaut M = 110 kg.
SOLUTION
If the cup were vacuum tight, the number of molecules leaving the surface would be the same as the number of molecules returning to the surface. The mass flow rate of the molecules hitting the surface is
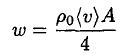 (1)
(1)
where ρ0 is the vapor density corresponding to the saturation, (v) is the average velocity of the molecules, and A is the surface area of the ice. The mass flow rate of the molecules actually returning to the surface is
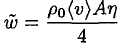 (2)
(2)
where η is the sticking coefficient (the probability that the molecule hitting the surface will stick to it). Let us assume for now that η = 1 (we will see later that this is not true, but that actually gives us the lower limit of the distance). If the cup is open we can assume that the number of molecules leaving the surface is the same as in the closed cup, but there are few returning molecules. We then find that the time τ for complete evaporation of the ice is
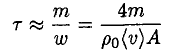 (3)
(3)
where we take m ~ 200 g as the mass of the ice, A ~ 30 cm2, and
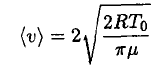 (4)
(4)
Substituting (4) into (3), we obtain
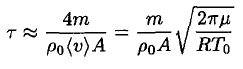 (5)
(5)
Once again using the ideal gas law, we may obtain ρ0:
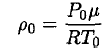 (6)
(6)
Substituting (6) into (5) yields
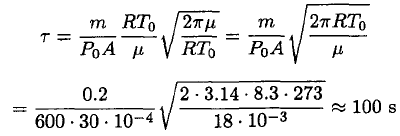 (7)
(7)
During the sublimation of the ice, the acceleration of the astronaut is
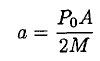 (8)
(8)
where P0A/2 corresponds to the momentum transferred by the molecules leaving the surface. Using the time τ calculated above, he will cover a distance
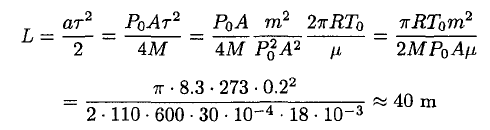 (9)
(9)
Note that this is the lower limit because we assumed η = 1 and that all the molecules that are leaving go to infinity. So, it seems that the astronaut can cover the distance to the ship by using his cup as an engine. Moreover, the sticking coefficient η, which is often assumed to be close to unity, could be much smaller (for water, η ~ 0.03 at 0°C). That explains why the water in a cup left in a room does not evaporate in a matter of minutes but rather in a few hours. For a detailed discussion see E. Mortensen and H. Eyring, J. Phys. Chem. 64, 846 (1960). The physical reason for such a small sticking coefficient in water is based on the fact that in the liquid phase the rotational degrees of freedom are hindered, leading to a smaller rotational partition function. So, the molecules whose rotation cannot pass adiabatically into the liquid will be rejected and reflect back into the gaseous phase. These effects are especially strong in asymmetric polar molecules (such as water). The actual time the teacup engine will be working is significantly longer (about 30 times, if we assume that the sticking coefficient for ice is about the same as for water at 0oC).



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|