


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 28-7-2016
Date: 9-8-2016
Date: 13-7-2016
|
Dielectric Cylinder in Uniform Electric Field
An infinitely long circular cylinder of radius a, dielectric constant ε, is placed with its axis along the z-axis, and in an electric field which would be uniform in the absence of the cylinder, E = E0 x (see Figure 1.1). Find
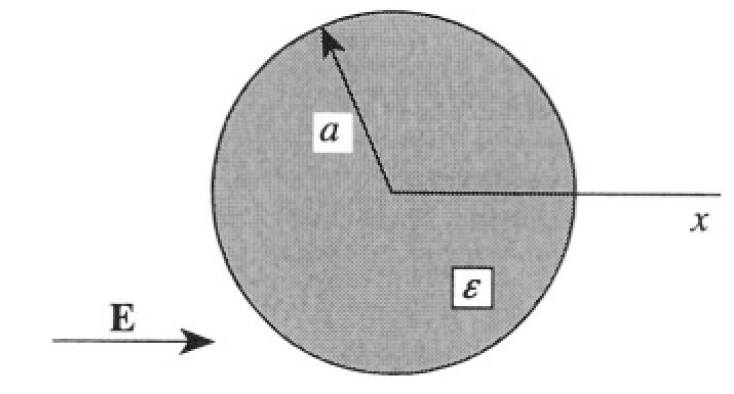
Figure 1.1
the electric field at points outside and inside the cylinder and the bound surface charge density.
SOLUTION
First solution: Introduce polar coordinates in the plane perpendicular to the axis of the cylinder (see Figure 1.2). In the same manner as,
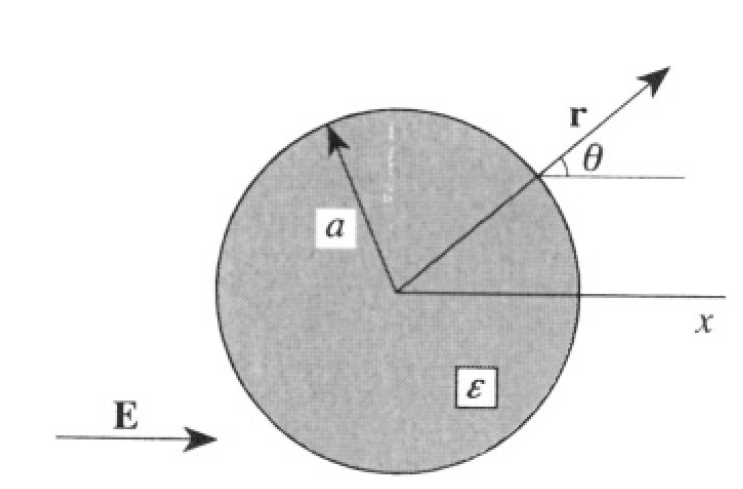
Figure 1.2
we will look for a potential outside the cylinder of the form
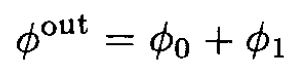 (1)
(1)
where ϕ0 = -E . r and ϕ1 is a solution of the two-dimensional Laplace equation, which may depend on one constant vector E
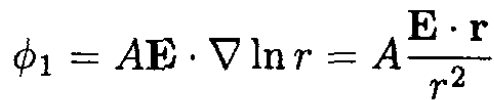 (2)
(2)
where A is some constant. Inside the cylinder, the only solution of Laplace’s equation that is bounded in the center of the cylinder and depends on E is
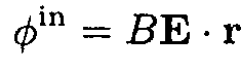
Using the condition on the potential ϕ at r = a, ϕin = ϕout we find
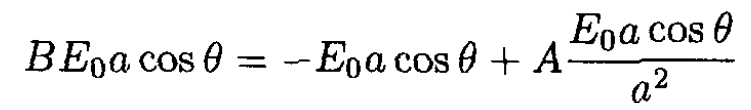 (3)
(3)
from which we find
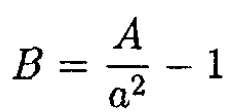
We now have
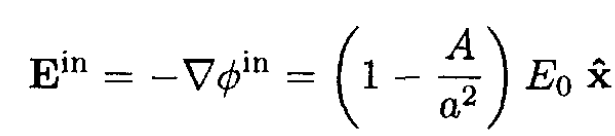 (4)
(4)
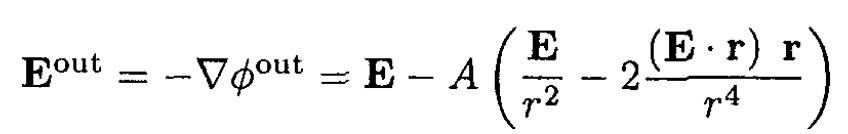 (5)
(5)
Using the boundary condition Dinn = Doutn or Einn = εEoutn, we find
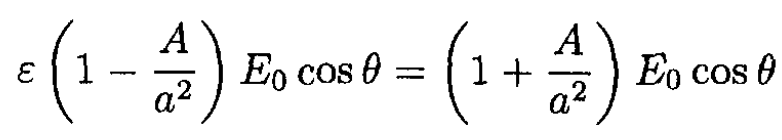
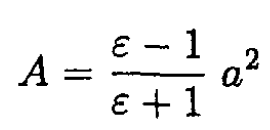
So we obtain
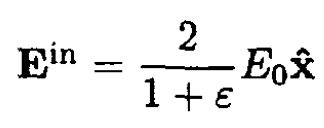 (6)
(6)
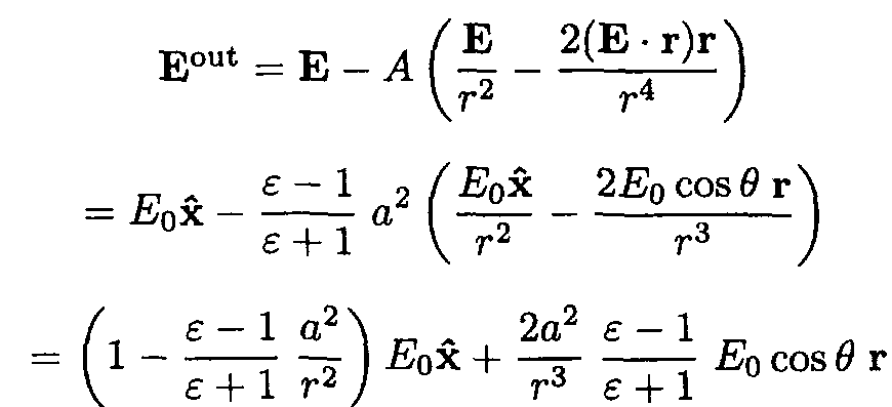 (7)
(7)
The polarization is
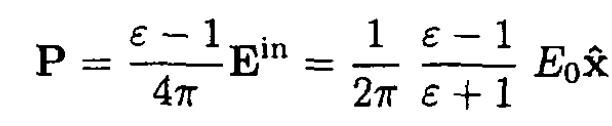
So the dipole moment per unit length of the cylinder is
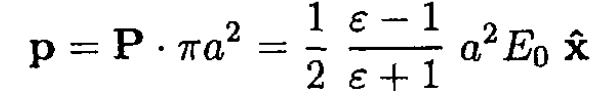
which corresponds to the potential
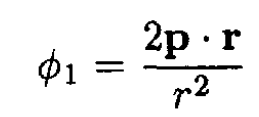
The surface charge density σ is
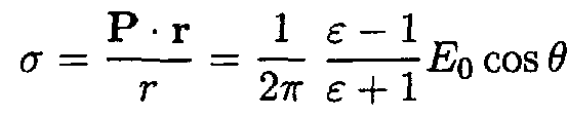
Second solution: Use the fact that for any dielectric ellipsoid with a dielectric constant ε immersed in a uniform electric field in vacuum, a uniform electric field inside is created. Therefore there must be a linear dependence between E0x, Einx, and Dinx, where the applied field E0 is along the x-axis
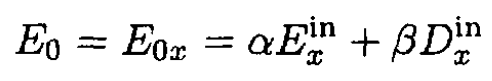 (8)
(8)
where α and β are coefficients independent of the dielectric constant of the ellipsoid and only depend on its shape. For the trivial case in which ε = 1
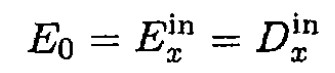
Therefore
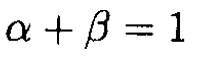 (9)
(9)
For a conducting ellipsoid (which can be described by a dielectric constant ε = ∞)
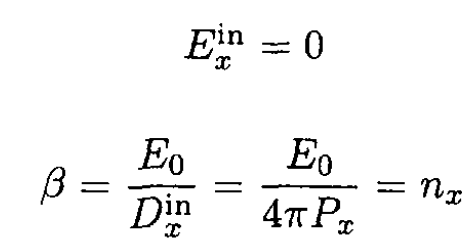
where nx is the depolarization factor. From (9), we have
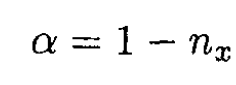
Finally (8) takes the form
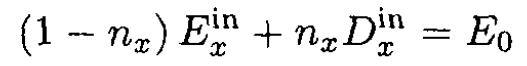 (10)
(10)
For a cylinder parallel to the applied field along the z-axis, nz = 0, but nx + ny +nz = 1, so nx = ny = 1/2. Equation (10) becomes
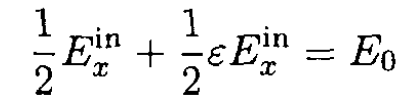 (11)
(11)
and
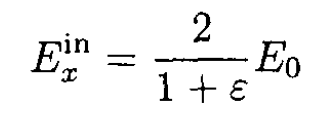 (12)
(12)
as in (6) above.



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|