


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 25-7-2016
Date: 9-8-2016
Date: 25-8-2016
|
Nonrelativistic Electron Gas
a) Derive the relation between pressure and volume of a free nonrelativistic electron gas at zero temperature.
b) The formula obtained in (a) is approximately correct for sufficiently low temperatures (the so-called strongly degenerate gas). Discuss the applicability of this formula to common metals.
SOLUTION
a) As τ → 0, the Fermi-Dirac distribution function
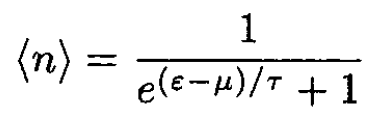 (1)
(1)
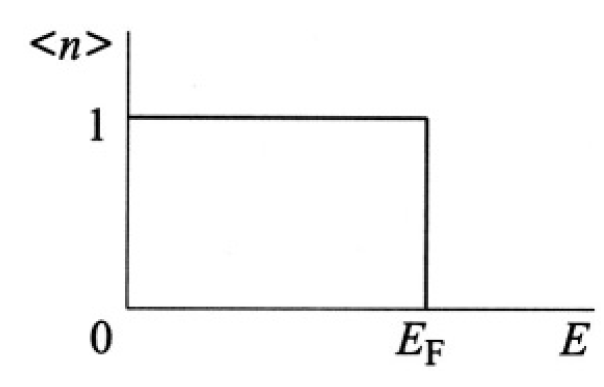
Figure 1.1
becomes a step function. All the states above a certain energy, ε > μ, are empty, and the states below, ε < μ, are filled (see Figure 1.1). This energy for an electron gas is called the Fermi energy. Physically, this results from the simple fact that the total energy of the gas should be a minimum. However, we have to reconcile this with the Pauli principle, which prohibits more than one electron per quantum state (i.e., same momentum and spin). This means that the states are filled gradually from zero energy to the limiting energy, εF. The number of states accessible to a free particle with absolute value of momentum between p and p + dp is
 (2)
(2)
In each of these states, we can put two electrons with opposite spin (up and down), so if we consider the total number of electrons, N, contained in a box of volume V, then N is given by
 (3)
(3)
Substituting p2/2m = ε, we obtain
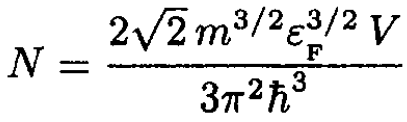 (4)
(4)
and therefore
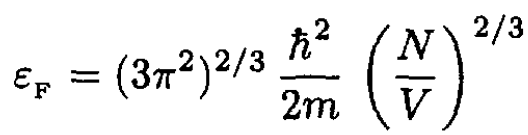 (5)
(5)
To calculate the total energy of the gas, we can write
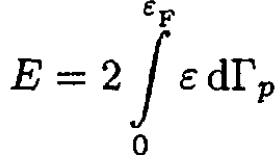
where again 
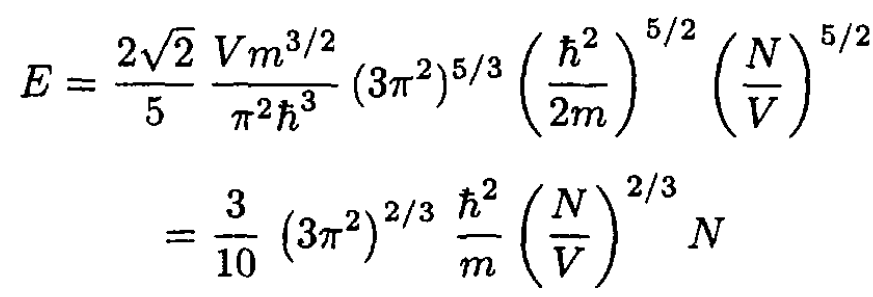 (6)
(6)
and therefore
 (7)
(7)
and we can check that
 (8)
(8)
b) The condition for strong degeneracy is that the temperature τ should be much smaller than the Fermi energy:
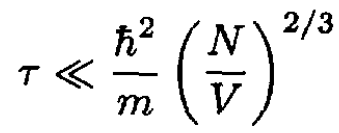 (9)
(9)
For typical metals, if we assume that there is one free electron per atom and a typical interatomic distance 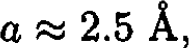 we obtain an electron density N/V
we obtain an electron density N/V  which indicates a Fermi energy of the order of
which indicates a Fermi energy of the order of 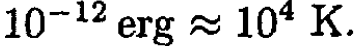 So, most of the metals are strongly degenerate, even at room temperature.
So, most of the metals are strongly degenerate, even at room temperature.



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
لحماية التراث الوطني.. العتبة العباسية تعلن عن ترميم أكثر من 200 وثيقة خلال عام 2024
|
|
|