


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 15-3-2021
Date: 21-8-2016
Date: 22-8-2016
|
London Penetration Depth
The model used by the brothers F. and H. London suggests that free electrons in a superconductor can be divided into two types: normal, with a density nn, and superconducting, with a density ns (where ns+ nn = n, the density of free electrons). On the surface of the superconductor flows a current with density Js.
a) Using classical arguments, obtain the equation for the electric field E, where
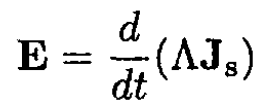 (i)
(i)
where Λ = m/(nse2). Here, m and e are the mass and charge of the electron. Again using classical arguments, write the kinetic energy of superconducting electrons in the form
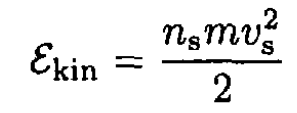
Adding the magnetic field energy, find a minimum of the free energy Fs(h) to obtain a second equation
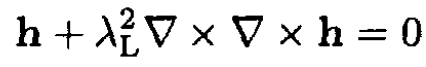 (ii)
(ii)
where h is a microscopic magnetic field inside the superconductor and is the London λL penetration depth.
b) Solve (2) for the boundary between vacuum and a space half filled with superconductor, with an external field H0 parallel to the boundary, and estimate λL (0) for a typical metal superconductor at zero temperature, assuming ns (0) = n.
SOLUTION
a) Equation (i) can be obtained from a naive classical model with a superconducting electron density ns. This derivation is not quite rigorous since we assume spatially uniform fields in the penetration depth. For a unit volume of superconducting electrons in an electric field E,
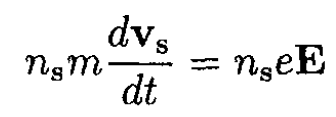 (1)
(1)
The superconducting current density may be written as Js = ns evs. Substituting into (1) gives (i):
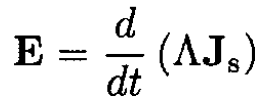
To derive (ii), write the kinetic energy density in the form
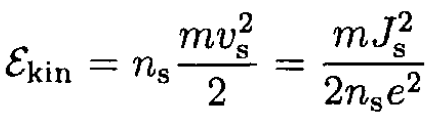
Using Maxwell’s equation
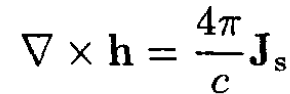
we obtain
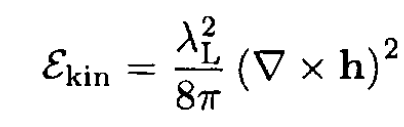 (2)
(2)
where
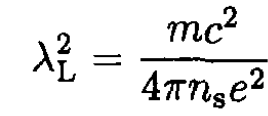 (3)
(3)
Now we can write the free energy in the form
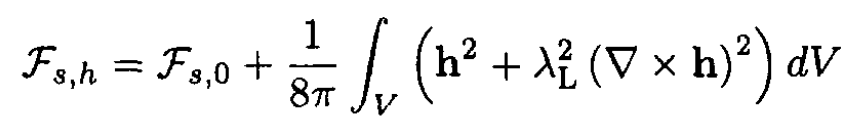
where ∫ h2/(8π)dV accounts for the energy of the magnetic field in the superconductor. We want to find a function h(r) that will minimize the free energy. Note that a more rigorous approach requires that we minimize the Gibbs’ free energy, but the result is the same. Using a standard procedure we take a variation of Fs, h. We can write
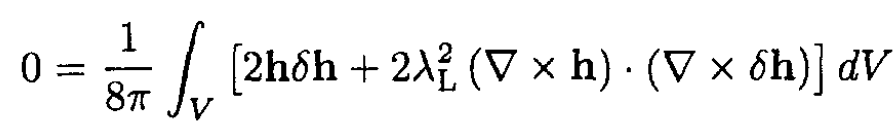 (4)
(4)
The second term in (4) can be transformed using the identity
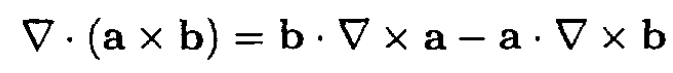
Now we can rewrite (4) in the form
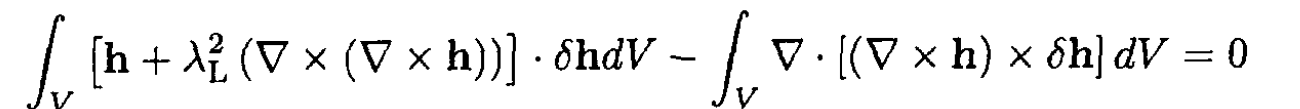 (5)
(5)
The second integral in (5) can be transformed into a surface integral using Gauss’s theorem
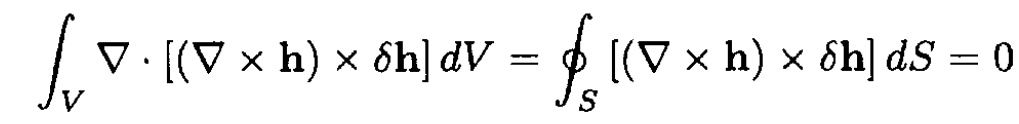
since everywhere on the surface h = H0, and so δh = 0. So, from the first integral in (5), we obtain (ii)
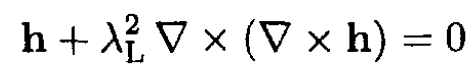
b) Using (ii) and the identity
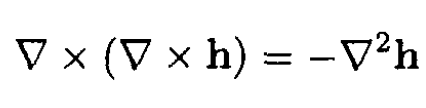
we have
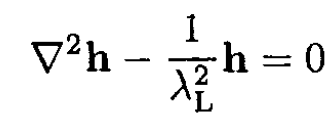
Orient the x direction normal to the boundary and the magnetic field parallel to it, H = H0 ẑ. From the symmetry of the problem, it is obvious that h = h(x) ẑ. Then (ii) becomes
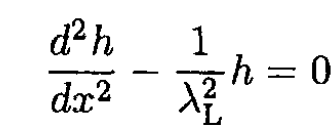
whose solution is
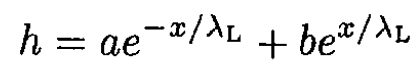
Invoking the boundary conditions h(0) = H0 and h (∞) = 0, we arrive at
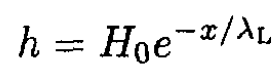
where λL is the London penetration depth introduced in (a) (2). For a typical metal superconductor with one free electron per atom
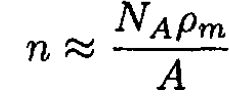
where NA is Avogadro’s number, ρm is the mass density, and A is the atomic mass in grams per mole. For a typical superconductor, n ≈ 1022 – 1023 cm-3. Assuming ns = n at T = 0, we have from (3)
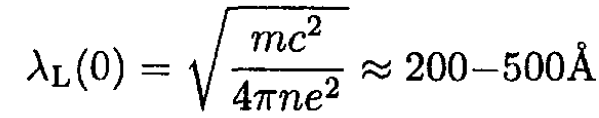



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|