


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 11-8-2016
Date: 14-8-2016
Date: 11-8-2016
|
Electrostatic Forces and Scaling
a) Consider two solid dielectric spheres of radius a, separated by a distance R(R >> a). One of the spheres has a charge q, and the other is neutral (see Figure 1.1a). We scale up the linear dimensions of the system by a factor of two. How much charge should reside on the first sphere now so that the force between the spheres remains the same?
b) Now consider a conducting ring made of thin wire, where d is the diameter of the wire and D is the diameter of the ring (again, D >> d) A charge Q placed on the ring is just sufficient to cause the ring to
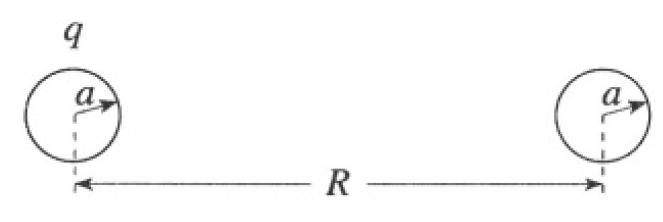
Figure 1.1a
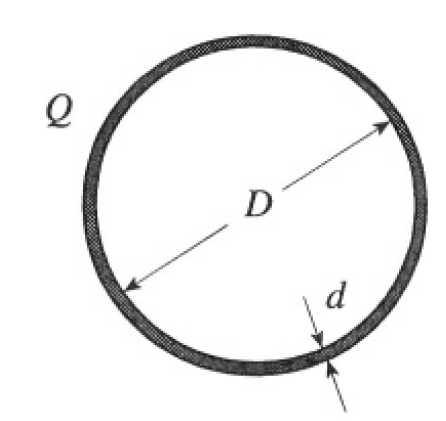
Figure 1.1b
break apart due to electrostatic repulsion (see Figure 1.1b). As in (a), the linear dimensions of the system are multiplied by two. At what charge will the new ring break?
SOLUTION
a) The charged sphere will polarize the neutral one, which acquires a dipole moment p proportional to the electric field created by the charged sphere
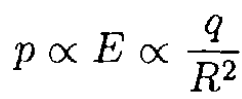
The force between the dipole and the charged sphere is given by the product of the dipole moment and the gradient of the electric field at the dipole:
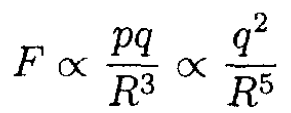
The condition that F = F' after increasing the distance by a factor of two gives for the new charge q'
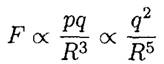
So
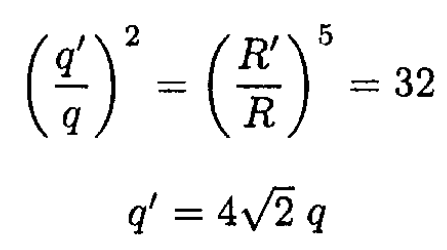
b) The charge Q will be distributed uniformly along the wire. So the Coulomb force between some point on the ring and the rest of the ring will be proportional to the square of Q and inversely proportional to the square of the diameter D of the ring
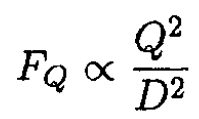 (1)
(1)
When the ring breaks, the elastic force Fe attempting to maintain the integrity of the ring is given by
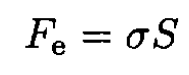 (2)
(2)
where σ is the ultimate strength, which depends only on the material of the wire, and S is the cross section of the wire. At the point when the ring parts, FQ = Fe, so equating (1) and (2), we obtain
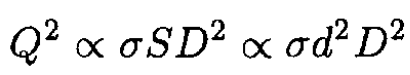
Scaling up the linear dimensions by a factor of two gives
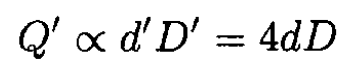
Therefore
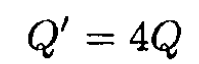



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|