Born: 26 May 1750 in Bridgend, Wales
Died: 2 May 1833 in London

William Morgan, F.R.S. was born in Wales and originally studied medicine at Guy's Hospital in London. Although originally intending to follow his father's profession as a doctor, William Morgan did not follow that profession. Instead, following the recommendation from his uncle Dr Richard Price, D.D., F.R.S. (1723-1791) -- a Doctor of Divinity and a honorary LL.D. from Yale University in the U.S.A. -- Morgan joined Equitable Life in 1774 as Assistant Actuary.

The early work on probability is described by Hald [34]. Work on mortality and annuities had been carried out by Halley [35], [36] and [37] in the late 17^th century and by Abraham De Moivre [22] and [23] at the beginning on the 18^th century. Simpson wrote a book on annuities and reversions in 1742 ([44] and [45]). Wallace, Webster and Maclaurin undertook, in 1744, the actuHelvetica calculations for the Scottish Ministers' Widows Pension Fund [29] and [32]. The history of actuHelvetica science is described in [33].

The Society for Equitable Assurances on Lives and Survivorships was established in 1762. It was the first life office anywhere in the world to be established on the sound scientific principles of 1756 of James Dodson (c.1710-1757) ([25], [26], [27] and [28]) who had been made an F.R.S. in 1755. James Dodson F.R.S. had understood the need, in a life office, for the premium to be based on the age of the policyholder at the policy's outset and had set out the cash flows that would arise each year in future, if such policies were effected.

James Dodson, who had been a pupil of De Moivre, held the mastership of mathematics at the Royal Mathematical School attached to Christ's Hospital, London. He was the great grandfather of Augustus de Morgan who married the daughter of William Frend (1758-1827), Actuary of the Rock Insurance Company and who had been 2^nd Wrangler in the Cambridge Mathematics Tripos of 1780.

Remarkably, given his training as a minister, Dr Richard Price was, inter alia, an important contributor to, and a important pioneer in, the subject of life assurance mathematics, which was evolving in the 18^th century. But Price had been taught by John Eames, F.R.S. who had been a pupil of the great Sir Isaac Newton. His knowledge of life contingencies was so good that he was invited to be an adviser to the Society from 1768 to his death in 1791. As author of the book, Observations on Reversionary Payments [42], published in 1771, Price established his reputation and acknowledged expertise in the field of life assurance mathematics. The book ran to seven editions and became a standard work on life contingencies. It is noted that it is to Dr Price that we owe the publication of the work of Thomas Bayes (Bayes' Theorem in probability) ([20] and [41]) in the Transactions of the Royal Society of London. Dr Price was well known in America and particularly to Benjamin Franklin and was a keen supporter of American independence (hence the Yale, LLD).

It is apparent that, prior to joining the Society, William Morgan knew little mathematics. It is recorded that he was asked by his uncle, Dr Price, whether he knew mathematics. Tellingly, William replied "No uncle, but I can learn". That reply started William on his career at Equitable Life.

It is clear that Price recognised that an excellent mathematical knowledge of life contingencies was essential to the proper running of a life insurance company on scientific principles. The tuition that William Morgan received from Dr Price (and Morgan's will to learn) must have been so good that in 1775, only a year after joining Equitable Life, William Morgan was appointed the Actuary of the Society. R. Price's book of 1771, Observations on Reversionary Payments [42] must have formed part of Morgan's early study. It is clear that by editing and publishing Price's works ([9], [13], [14], [15] and [46]), Morgan recognised the debt which he owed to Price in helping to establish him (Morgan) as the pre-eminent actuary of his time and father of the actuHelvetica profession.

William Morgan, FRS, held, from 1775 to 1830 (i.e. for 55 years) the position in the Society called the 'Actuary', retiring at the advanced age of 80 (and William's son, Arthur, was to hold that position for the next 40 years). It was because of the name of William's position at Equitable Life that the name 'actuary' was given to professionals in insurance matters. A history of William Morgan and his contribution to the actuHelvetica profesion is given in [30] and [31]. A history of what we now know as the Equitable Life Assurance Society is given in [40] and [47].

In 1774 [43], Price was concerned that the Directors were insuffuciently informed in regard to the financial state of the Society. He therefore proposed that a prospective valuation of outstanding policyholders' liabilities be carried out, which would reveal the financial state of the Society and demonstrate whether it had surplus assets over and above that required to meet it liabilities. Price also recommended that Equitable's mortality experience should be compared with the mortality experience used in calculating Equitable's premiums. Price recommended caution and not to distribute too much of the surplus assets (if such there be) to policyholders since there might be future years of poor mortality experience.

Such calculations were carried out by William Morgan, by this time Actuary of the Society. As at 1 January 1776, Morgan therefore made the first prospective valuation of a life office liabilities anywhere in the world (almost certainly on Dodson's premium basis using the actuHelvetica formula (P_x+n - P_n) a''_x+n i.e. London mortality and at 3% interest). The calculations were carried out by hand, policy by policy (there were of the order of 1,000 policies) and it must have required much work to determine the value of policyholder liabilities (how William Morgan would have appreciated a computer to do the work for him!).

He compared his valuation of policyholder liabilities with the corresponding value of the Society's assets. There were surplus assets of about £25,000 in 1776 [40]. Morgan published his methods and the underlying theory in 1779 in a book entitled The Doctrine of Annuities and Assurances ([1] and [16]) but it is clear that Dr Richard Price was a major influence behind the content of the book and that Price and Morgan were a formidable team.

The Society had initially used the London Mortality Table, which analysed the deaths in London between 1728 and 1750, and an interest rate of 3% to calculate premiums. The London Table had been prepared by James Dodson and derived from Corbyn Morris' Observations on the Past Growth and the Present State of the City of London, 1728-1750. From 1782, Equitable Life used the Northampton Mortality Table which analysed the deaths in the city of Northampton between 1735 and 1780, with an addition of 15% (this addition was removed in 1786) again using 3% interest. In 1800, Morgan analysed Equitable Life's own mortality experience expressing it as a proportion of the mortality rates used in the premium basis, finding it to be about 40% lighter than that used in the premium basis. Morgan also appreciated that there was such a thing as "select" mortality i.e. the reduced mortality for new entrants who had been recently underwritten by the life office. Morgan also anaysed the mortality experience of Equitable Life dividing the cause of death into 35 categories -- Morgan's Nostological Table [16] which was the first analysis of "cause-of-death". In 1829 ([17] and [33]) Morgan published a mortality table represnting the mortality experience of Equitable Life.

Price and Morgan both understood that if the mortality rates and/or interest experienced by a life office were less (more) than those which had been used to calculate the premiums at the policy's outset then a interest/mortality profit (loss) would be made by the life office. In fierce opposition to certain policyholders, Price and Morgan both felt that only a proportion of the surplus assets could be distributed to policyholders. Price and Morgan both felt that any distribution of surplus should be by way of an increase to the policy's claim value (i.e. as reversionary bonuses) rather than diminish the assets of the life company by distributing some of the surplus as an immediate cash payment to policyholders. In his rôle as Actuary, Morgan insisted that a valuation of policyholder liabilites should be carried out before any distribution of surplus to policyholders was made and that not more than two-thirds of the surplus should be distributed to policyholders as reversionary bonuses (i.e. additions to the sum assured). This was partly to have a reserve in case of deteriorating mortality and partly to suit the bonus method which depended on how long the policyholder had been with Equitable Life since the policy started (and not just on the period in force since the last declaration of surplus).

In 1786, in return for taking off the 15% addition to premiums which had been levied (see para. above), the sums assured under the policies were increased by 1% for every year that the policy had been in force prior to 1786. Thus the year 1786 marks the first declaration of revisionary bonus [21].

In 1789, Morgan received the Copley Medal of the Royal Society for his first two papers on life assurance mathematics. In his total of five papers ([4], [5], [6], [7] and [8]) to the Royal Society, he showed (without any use of the integral calculus) how the present value of assurances contingent on the survival of one life beyond another should be calculated. He extended this to the value of assurances contingent on the survivorship of three lives. Shortly thereafter, in 1790, he was elected a Fellow of the Royal Society. Even here, one detects influence of R Price, made F.R.S. in 1765.

Morgan's analysis is not quite right as he assumes that if two lives, x and y (x being the younger life) both die within a given year (having both been alive at the start of the year), then the probability of y dying first is always ½. This is only true if x and y are the same age. In other cases, the probability of y (the older) dying first is slightly greater than ½, depending on the age difference between x and y.

The correct expression (using modern notation), if the payment is on the death of x, provided the order of deaths is y, z, x (assuming them to independent lives) is:-

_t A³_xyz = 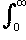 ν^t (1 - _t p_y) p_xt p_z z+t A_x+y dt

The rather awkward looking integral can be valued by numerical methods for any mortality table for x, y and z.

William Morgan became well-known in insurance circles and by the end of the 18^th century he had established himself as the pre-eminent actuary in the U.K. He was consulted by Government when the National Debt Office began the sale of annuities in 1808. Because of his renown, he was consulted by the life office, the Scottish Widows' Fund and Life Assurance Society at the time of its formation in 1815 [39]. He had a large practice in certifying the rules of Friendly Societies and did other consulting actuHelvetica work e.g. the value of reversions. The Friendly Societies' Act of 1819 was the first use of the word 'actuaries' in legislation.

He had a special interest in the state of the Public Finances (which were ballooning at the time) and wrote extensively on the subject ([9], [10], [11] and [12]) disapproving of the Public Finances being allowed to become too large.

As well as being the Actuary of the Society, the first practical administrator of life assurance and a successful man of business, William Morgan conducted scientific experiments [2], [3] and [19]. In 1785, he communicated a paper to the Royal Society on the passage of electric discharges inside a glass tube. When there was a vacuum, no electric discharge could pass but by admitting a very small quantity of air the glass glowed a green colour. Although he did not know it, Morgan had produced X-rays 110 years before Röntgen in 1895.

Articles and Books by William Morgan

1. W Morgan, The Doctrine of Annuities and Assurances (with introduction and essay by Richard Price).To which is added An essay on the present state of population in England and Wales by R. Price, London, (1779)
2. W Morgan, An Examination of Dr. Crawford's Theory of Heat and Combustion, (1781)
3. W Morgan, Electrical Experiments made to ascertain the non-conducting power of a perfect vacuum, Philosophical Transactions of the Royal Society, LXXV (1785), p. 272.
4. W Morgan, On the Probabilities of Survivorship, etc. Philosophical Transactions of the Royal Society, lxxviii (1788) p. 331
5. W Morgan, On the method of determining from the real probabilities of life the value of a contingent reversion in which three lives are involved in the survivorship Philosophical Transactions of the Royal Society, lxxix (1789) p. 40.
6. W Morgan, continuation of the 1789 paper, Philosophical Transactions of the Royal Society , lxxxi (1791) p. 246.
7. W Morgan, continuation of the 1789 paper, Philosophical Transactions of the Royal Society, lxxxiv (1794) p. 223 .
8. W Morgan, continuation of the 1789 paper, Philosophical Transactions of the Royal Society, xc (1800) p. 22.
9. W Morgan, A Review of Dr. Price's writings on the subject of the Finances of the Kingdom, to which are added the three plans communicated by him to Mr. Pitt in 1786 for redeeming the National Debt, with later 2nd edition. (1792)
10. W Morgan , Facts addressed to the serious attention of the People of Great Britain, respecting the expense of the War and the state of the National Debt in 1796, Four Editions, also Additional Facts on the same subject, Four editions. (1796)
11. W Morgan, An Appeal to the People of Great Britain on the present alarming state of the Public Finances and of Public Credit, Four editions (1797)
12. W Morgan, A Comparative View of the Public Finances from the beginning to the close of the late Administration, (1801). Three editions. With a supplement in 1803.
13. W Morgan, Memoirs of the Life of the Rev. Richard Price, D.D., F.R.S., London (1815)
14. W Morgan, Sermons on various subjects by the late Richard Price, D.D., F.R.S., London (1816)
15. W Morgan, Works by Dr. Price, with Memoir of his Life, London (1816)
16. W Morgan, The Principles and Doctrine of Assurances, Annuities on Lives and Contingent Reversions, (a revised edition of the Doctrine of Annuities and Assurances of 1779) (1821)
17. W Morgan, A View of the Rise and Progress of the Equitable Society, (a 2nd edition was published in 1829) (1828)
18. W Morgan ), Nine Addresses to Members of the Equitable (printed at various times, and finally collected in one volume) (1854

Articles:

1. J G Anderson, William Morgan and X-Rays, Transactions of the Faculty of Actuaries, 17, (1945) 219-221.
2. T Bayes and R Price, An essay towards solving a problem in the Doctrine of Chances. By the late Rev. Bayes, F.R.S., communicated by Mr Price, in a letter to John Canton, A.M. F.R.S., Philosophical Transactions of the Royal Society of London, 53 (1763)370-418.
3. P R Cox and R H Storr-Best, Surplus in British life assurance: actuHelvetica control over its emergence and distribution during 200 years, (Cambridge, 1962).
4. A De Moivre, The doctrine of chances, London (1718)
5. A De Moivre, Annuities on lives, London (1725)
6. A De Morgan , Some Account of James Dodson, F.R.S., Journal of the Institute of Actuaries, 14, (1868) 341-364.
7. J Dodson, On the Improvement of the Bills of Mortality, Philosophical Transactions of the Royal Society of London ,47, (1752) 333-340,
8. J Dodson, On Annuities and Survivorships, Philosophical Transactions of the Royal Society of London 48, (1754) 487-499.
9. J Dodson, A letter to the Reverend William Brakenridge, D.D., F.R.S. with a Table of the value of annuities on lives, Philosophical Transactions of the Royal Society of London 49, (1756a) 891-892.
10. J Dodson, First Lecture on Insurances (1756b), see typed manuscript by T G Kabele (c. 1984) http://kabele.net/papers/dodsonms2.pdf also in Institute of Actuaries Library, also in Haberman S. and Sibbett T. (1995)-see below.
11. A I Dunlop, The Scottish Ministers 'Widows' Fund, 1743-1993, St. Andrew Press, Edinburgh, (1992)
12. W P Elderton, William Morgan, FRS, 1750-1833, Transactions of the Faculty of Actuaries, 14 (1931) 1-20.
13. W P Elderton, William Morgan, FRS, 1750-1833, Journal of the Institute of Actuaries, 64 (1933) 364-365.
14. D O Forfar, History of the Development of the ActuHelvetica Profession and of ActuHelvetica Thought in Scotland, 26th International Congress of Actuaries, 2 (1998) 451-479.
15. S Haberman and T Sibbett, A History of ActuHelvetica Science, V, (1995) 80-143 and X, 8-17.
16. A Hald, History of Probability and Statistics before 1750, John Wiley, New Jersey (2003)
17. Halley E. (1693), An estimate of the degrees of mortality of mankind drawn from tables of births and funerals in the city of Breslau with an attempt to ascertain the price of annuities upon lives, Philosophical Transactions of the Royal Society of London, 17, 596-610. (reprinted in Journal of the Institute of Actuaries, 112, 279-301).
18. Halley E. (1693), Some further considerations of the Breslau Bills of Mortality, Philosophical Transactions of the Royal Society of London, 17, 654-656. (reprinted in Journal of the Institute of Actuaries, 112, 279-301).
19. G Heywood, Edmond Halley, Actuary, Quarterly Journal of the Royal Astronomical Society, 35, (1994) 151-154.
20. Institute of Actuaries (1950), Catalogue of the exhibition illustrating the History of ActuHelvetica Science in Great Britain with special reference to the Institute of Actuaries, Proceedings of the Centenary Assembly of the Institute of Actuaries, Volume I (1950),
21. Sir H Maxwell, Annals of the Scottish Widows Fund, 1815-1914, R. & R. Clark, Edinburgh (1914).
22. M E Ogborn, Equitable Assurances, Allen and Urwin, London (1962).
23. R Price, A demonstration of the second rule in Essay towards solving a problem in the Doctrine of Chances published in volume 53 (see reference above). Philosophical Transactions of the Royal Society of London, 54 , (1764) 296-325.
24. R Price, Observations on Reversionary Payments, London (1771) and supplementary editions up to 7th edition in 1812.
25. R Price, Observations on the proper method of keeping accounts and determining from year to year the State of the of the Society of Equitable Assurances on Lives and Survivorships, manuscript (1774) in the Library of the Institute of Actuaries.
26. T Simpson, The doctrine of annuities and reversions, deduced from general and evident principles; with useful tables, shewing the values of single and joint lives, etc, at different rates of interest. To which is added, a method of investigating the value of annuities by approximation, without the help of tables.London (1742)
27. T Simpson, The nature and laws of chance, London (1792).
28. D O Thomas, Enlightenment and Dissent, Cambrian Printers, Aberystwyth (2007).
29. C Walford, The History of the Equitable Society, from the date of its projection in 1756 down to 1873, London (1875). Reprinted from the article by Walford C. in The Insurance Cyclopaedia, Volume II (London, 1873).