RESONATOR    STABILITY

      The most general form of a laser cavity, is one consisting of two concave mirrors with coincident foci in the center of the laser medium. This is contrary, perhaps, to popular opinion, which is usually that two plane mirrors are used, although that arrangement, too, is stable (although only marginally) and is employed in some lasers. In the confocal arrangement, a true Gaussian beam traverses between the concave mirrors, and it can be found in which the curvature of the wave front of the intracavity beam approaching the mirrors matches the curvature of the cavity mirrors themselves. This ensures that the beam reflects perfectly back on itself and is completely trapped within the cavity the definition of stability. Any ray within the cavity can retrace itself exactly after one round trip through the cavity. If one mirror is partially transmitting, the beam that passes through the mirror (which becomes the output beam) continues to diverge.

         We now examine the parameters behind the design of resonators in order that one may be designed to confine radiation properly in the laser. The vast majority of lasers use stable resonator configurations, those in which light between the mirrors

Figure 1.1. Parameters for resonator stability.

is trapped completely and the beam is reflected back on itself within the cavity, keeping the power density large, to encourage stimulated emissions. To determine stability (mathematically) we introduce resonator g parameters, one representing each mirror, which define the beam path relative to the entire cavity. Knowing the distance between the cavity mirrors as well as the radius of curvature for a mirror, the expression for a g parameter is

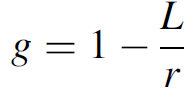 (1.1)

where L is the distance between the cavity mirrors and r is the radius of curvature. These parameters are defined in Figure 1.1, which shows a generalized laser cavity with concave mirrors. Stability, then, is defined as the condition where

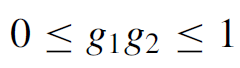  (1.2)

where g1 and g2 are the g parameters for each mirror. In the case of a plane mirror, the radius is infinity, so the corresponding g parameter is 1.

Example 1.1 Resonator Stability Consider a laser cavity consisting of two spherical mirrors resembling that of Figure 1.1. The distance between the two mirrors is 1 m and each mirror has a radius of 60 cm. Using equation (1.1), the g parameter for each mirror is calculated to be 1-1/0.6 = 20.67, so that the product of the g parameters is 0.44. This resonator arrangement is hence found to be stable.

      Consider a similar second cavity where each mirror has a radius of 45 cm. The g parameter of each mirror is now calculated to be -1.22, so that the product of the g parameters is 1.49. Since this value is greater than 1, the configuration is not stable. Various cavity arrangements are examined in the next section.

      It must also be noted that some cavity arrangements utilize the lasing volume better than others. A confocal cavity, for example, uses only a fraction of the gain medium, whereas a cavity consisting of two plane mirrors can use much more of the gain medium, presumably allowing higher efficiency and power output. A cavity consisting of two plane mirrors, however, is difficult to align (it presents marginal stability, as the product of the g parameters is exactly 1), so most practical laser cavities consist of one or more concave or spherical mirrors, as we examine in the next section. It is also possible to use intracavity beam expanders (consisting of two or more lenses) to improve utilization of the entire volume of the lasing medium (this is sometimes done in YAG lasers to ensure use of the entire rod).