


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-2-2016
Date: 20-2-2016
Date: 23-2-2016
|
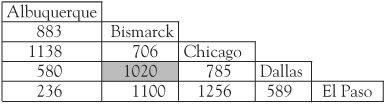
James Cook, based in Bismarck (North Dakota, USA), is a super salesperson for the Electra company, a manufacturer of carpet cleaners. The fact that he has won salesperson of the year for three years straight is evidence of his ability. His sales area takes in the cities of Albuquerque, Chigaco, Dallas and El Paso, and he visits each of them in a round trip once a month. The question he sets himself is how to make the trip and at the same time minimize the total mileage travelled. It is the classical travelling salesperson problem.
James has drawn up a mileage chart showing distances between the cities. For example, the distance between Bismarck and Dallas is 1020 miles, found at the intersection (shaded) of the Bismarck column with the Dallas row.
The greedy method
Being a practical person, James Cook sketches a map of the sales area but doesn’t worry about accuracy so long as it tells him roughly where the cities are and the distances between them. One route he often takes starts from Bismarck travelling to Chicago, Albuquerque, Dallas and El Paso in turn before returning to Bismarck. This is the route BCADEB but he realizes this trip of 4113 miles in total is expensive in terms of the distance travelled. Can he do better?
Making a plan of the sales area should not disguise the fact that James is not in the mood for detailed planning – he wants to get out there and sell. Looking at a map in his office in Bismarck he sees that the nearest city is Chicago. It is 706 miles away as against 883 to Albuquerque, 1020 miles to Dallas, and 1100 miles to El Paso. He starts for Chicago immediately without an overall plan. When he gets to Chicago and completes his business there he looks for the nearest city to go to. He chooses Dallas in preference to Albuquerque and El Paso, because it is 785 miles from Chicago, and is nearer than the other options.
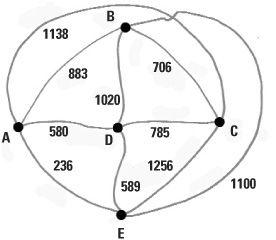
Once in Dallas he has notched up 706 + 785 miles. He then has to choose between Albuquerque and El Paso. He chooses Albuquerque because it is closer. From Albuquerque he has to go to El Paso whereupon he has visited all the cities and, job done, he returns to Bismarck. His total mileage is 706 + 785 + 580 + 236 + 1100 = 3407 miles. This route BCDAEB is much shorter than his previous route and he has made a saving on carbon emissions too.
This way of thinking is often called the greedy method of finding a short route. This is because James Cook’s decision is always a local one – he is in a certain city and looks for the best route out of that city. With this method he never attempts to look forward by more than one step at a time. It is not strategic because it takes no overall account of the best route. The fact that he finished in El Paso meant he was forced to take a long route back to Bismarck. So a shorter route has been found, but is it the shortest route? James is intrigued.
James sees how he can take advantage of there being only five cities involved. With so few it is possible to list all the possible routes and to then select the shortest one. With five cities there are only 24 routes to examine or just 12 if we count a route and its reverse as equivalent. This is permissible because both have the same total mileage. The method serves James Cook well and he learns that the route BAEDCB (or its reverse BCDEAB) is actually optimum, being only 3199 miles long.
Back in Bismarck James realizes his travel is taking too long. It is not the distance he wants to save, but time. He draws up a new table that gives the travel time between the different cities in his territory.
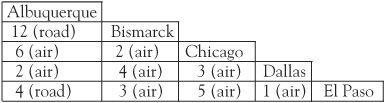
When the problem was focused on mileages, James knew that the sum of the distances along two sides of a triangle is always greater than the length of the third side; in this case the graph is called Euclidean and much is known about solution methods. This is not the case when the problem is one of time. Flying on main routes is often faster than side routes and James Cook notes that in going from El Paso to Chicago it is quicker to fly via Dallas. The so-called triangle inequality does not apply.
The greedy method applied to the time-problem produces a total time of 22 hours on the route BCDEAB, whereas there are two distinct optimum routes BCADEB and BCDAEB totalling 14 hours each. Of these two routes, the first is 4113 miles, and the second 3407 miles. James Cook is happy that by choosing BCDAEB he has saved the most. As a future project he will consider the route with least cost.
From seconds to centuries
The real difficulty associated with the travelling salesperson problem occurs when there is a large number of cities. Because James Cook is such a brilliant employee it is not long before he is promoted to being a supervisor. He now has to visit 13 cities from Bismarck instead of the previous 4. He is unhappy about using the greedy method, and prefers to look at a complete listing of the routes. He sets out to list the possible routes for his 13 cities. He soon discovers there would be as many as 3.1 x 109 routes to examine. Put another way, if a computer took one second to print out a route it would take about a century to print them all. A problem with 100 cities as input would tie up the computer for millennia.
Some sophisticated methods have been applied to the travelling salesperson problem. Exact methods have been given which apply to 5000 cities or less and one has even successfully dealt with a particular problem of 33,810 cities, though the computer power required in this case was colossal. Non-exact methods produce routes which are within range of the optimum with a specified probability. Methods of this type have the advantage of being able to handle problems with millions of cities.
Computational complexity
Looking at the problem from a computer’s point of view, let’s just think about the time it might take to find a solution. Simply listing all possible routes is a worst case scenario. James has discovered that this brute force method for 13 cities would take almost a century to complete. If we threw in an extra 2 cities the time would go up to over 20,000 years!
Of course these estimates will depend on the actual computer used, but for n cities the time taken rises in line with n factorial (the number you get by multiplying together all whole numbers from 1 to n). We calculated 3.1 × 109 routes for 13 cities. Deciding whether each route is the shortest yet found becomes a problem of factorial time – and it will be a long time.
Other methods are available for attacking the problem in which the time for n cities rises with 2n (2 multiplied by itself n times) so for 13 cities this would involve the order of 8192 decisions (8 times more than for 10 cities). A method with this complexity is called an exponential time algorithm. The holy grail of these ‘combinatorial optimization problems’ is to find an algorithm which depends not on the nth power of 2, but on a fixed power of n. The smaller the power the better; for example, if the algorithm varied according to n2 then, in the case of 13 cities, this would amount to only 169 decisions – less than twice the time taken for 10 cities. A method of this ‘complexity’ is said to be conducted in polynomial time – problems solved this way are ‘quick problems’ and could take 3 minutes, rather than centuries.
The class of problems that can be solved by a computer in polynomial time is denoted by P. We don’t know if the travelling salesperson problem is one of these. No one has come up with a polynomial time algorithm for it but nor have they been able to show that none exists.
A wider class denoted by NP consists of problems whose solutions can be verified in polynomial time. The travelling salesperson problem is definitely one of these because checking whether a given route is a shorter distance than any given distance can be done in polynomial time. You just add the distances along the given route and compare it with the given number. Finding and verifying are two different operations: for instance, it is easy to verify that 167 × 241 = 40,247 but finding the factors of 40,247 is a different proposition.
Is every problem verifiable in polynomial time able to be solved in polynomial time? If this were true the two classes P and NP would be identical and we could write P = NP. Whether P = NP is the burning question of the day for computer scientists. More than half the profession think this is not true: they believe there are problems out there that can be checked in polynomial time but cannot be solved in polynomial time. It is such an outstanding problem that the Clay Mathematics Institute has offered a prize of $1,000,000 to prove whether P = NP or P NP.
The condensed idea
Finding the best route




|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|