Common sense is not always a reliable guide. We shall see whether Euclid’s assumption makes mathematical sense.

Euclid’s Elements

Euclid’s geometry is set out in the 13 books of the Elements, written around 300 BC. One of the most influential mathematics texts ever written, Greek mathematicians constantly referred to it as the first systematic codification of geometry. Later scholars studied and translated it from extant manuscripts and it was handed down and universally praised as the very model of what geometry should be.

The Elements percolated down to school level and readings from the ‘sacred book’ became the way geometry was taught. It proved unsuitable for the youngest pupils, however. As the poet A.C. Hilton quipped: ‘though they wrote it all by rote, they did not write it right’. You might say Euclid was written for men not boys. In English schools, it reached the zenith of its influence as a subject in the curriculum during the 19th century but it remains a touchstone for mathematicians today.

Euclid’s postulates

One of the characteristics of mathematics is that a few assumptions can generate extensive theories. Euclid’s postulates are an excellent example, and one that set the model for later axiomatic systems. His five postulates are:

1. A straight line can be drawn from any point to any point.

2. A finite straight line can be extended continuously in a straight line.

3. A circle can be constructed with any centre and any radius.

4. All right angles are equal to each other.

5. If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if extended indefinitely, meet on that side on which the angles are less than two right angles.

It is the style of Euclid’s Elements that makes it noteworthy – its achievement is the presentation of geometry as a sequence of proven propositions. Sherlock Holmes would have admired its deductive system which advanced logically from the clearly stated postulates and may have castigated Dr Watson for not seeing it as a ‘cold unemotional system’.

While the edifice of Euclid’s geometry rests on the postulates (what are now called axioms; see box), these were not enough. Euclid added ‘definitions’ and ‘common notions’. The definitions include such declarations as ‘a point is that which has no part’ and ‘a line is breadthless length’. Common notions include such items as ‘the whole is greater than the part’ and ‘things which are equal to the same thing are also equal to one another’. It was only towards the end of the 19th century that it was recognized that Euclid had made tacit assumptions.

The fifth postulate

It is Euclid’s fifth postulate that caused controversy over 2000 years after the Elements first appeared. In style alone, it looks out of place through its wordiness and clumsiness. Euclid himself was unhappy with it but he needed it to prove propositions and had to include it. He tried to prove it from the other postulates but failed.

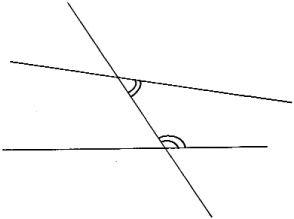
Later mathematicians either tried to prove it or replace it by a simpler postulate. In 1795, John Playfair stated it in a form which gained popularity: for a line l and a point P not on the line l there is a unique line passing through P parallel to l. Around the same time, Adrien Marie Legendre substituted another equivalent version when he asserted the existence of a triangle whose angles add up to 180 degrees. These new forms of the fifth postulate went some way to meet the objection of artificiality. They were more acceptable than the cumbersome version given by Euclid.

Another line of attack was to search for the elusive proof of the fifth postulate. This exerted a powerful attraction on its adherents. If a proof could be found, the postulate would become a theorem and it could retire from the firing line. Unfortunately attempts to do this turned out to be excellent examples of circular reasoning, arguments which assume the very thing they are trying to prove.

Non-Euclidean geometry

A breakthrough came through the work of Carl Friedrich Gauss, János Bolyai and Nikolai Ivanovich Lobachevsky. Gauss did not publish his work, but it seems clear he reached his conclusions in 1817. Bolyai published in 1831 and Lobachevsky, independently, in 1829, causing a prority dispute between these two. There is no doubting the brilliance of all these men. They effectively showed that the fifth postulate was independent of the other four postulates. By adding its negation to the other four postulates, they showed a consistent system was possible.

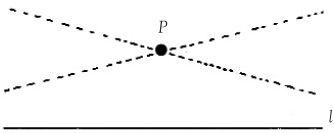
Bolyai and Lobachevsky constructed a new geometry by allowing there to be more than one line through P that does not meet the line l. How can this be? Surely the dotted lines meet l. If we accept this we are unconsciously falling in with Euclid’s view. The diagram is therefore a confidence trick, for what Bolyai and Lobachevsky were proposing was a new sort of geometry which does not conform to the commonsense one of Euclid. In fact, their non-Euclidean geometry can be thought of as the geometry on the curved surface of what is known as a pseudosphere.

The shortest paths between the points on a pseudosphere play the same role as straight lines in Euclid’s geometry. One of the curiosities of this non-Euclidean geometry is that the sum of the angles in a triangle is less than 180 degrees. This geometry is called hyperbolic geometry.

Another alternative to the fifth postulate states that every line through P meets the line l. Put a different way, there are no lines through P which are ‘parallel’ to l. This geometry is different from Bolyai’s and Lobachevsky’s, but it is a genuine geometry nevertheless. One model for it is the geometry on the surface of a sphere. Here the great circles (those circles that have the same circumference as the sphere itself) play the role of straight lines in Euclidean geometry. In this non-Euclidean geometry the sum of the angles in a triangle is greater than 180 degrees. This is called elliptic geometry and is associated with the German mathematician Benhard Riemann who investigated it in the 1850s.

The geometry of Euclid which had been thought to be the one true geometry – according to Immanuel Kant, the geometry ‘hard-wired into man’ – had been knocked off its pedestal. Euclidean geometry was now one of many systems, sandwiched between hyperbolic and elliptic geometry. The different versions were unified under one umbrella by Felix Klein in 1872. The advent of non-Euclidean geometry was an earth-shaking event in mathematics and paved the way to the geometry of Einstein’s general relativity . It is the general theory of relativity which demands a new kind of geometry – the geometry of curved space–time, or Riemannian geometry. It was this non-Euclidean geometry which now explained why things fall down, and not Newton’s attractive gravitational force between objects. The presence of massive objects in space, like the Earth and the Sun cause space–time to be curved. A marble on a sheet of thin rubber will cause a small indentation, but try placing a bowling ball on it and a great warp will result.

This curvature measured by Riemannian geometry predicts how light beams bend in the presence of massive space objects. Ordinary Euclidean space, with time as an independent component, will not suffice for general relativity. One reason is that Euclidean space is flat – there is no curvature. Think of a sheet of paper lying on a table; we can say that at any point on the paper the curvature is zero. Underlying Riemannian space–time is a concept of curvature which varies continuously – just as the curvature of a rumpled piece of cloth varies from point to point. It’s like looking in a bendy fairground mirror – the image you see depends on where you look in the mirror.

No wonder that Gauss was so impressed by young Riemann in the 1850s and even suggested then that the ‘metaphysics’ of space would be revolutionized by his insights.

the condensed idea

What if parallel lines do meet?