The Cratchits lived in a drab terrace house in Bayham Street, Camden Town just north of the newly opened University College, where De Morgan was professor. The source of the gift would have become clear in the new year when the professor called to see if Tim had coloured the map.

De Morgan had definite ideas on how this should be done: ‘you are to colour the map so that two counties with a common border have different colours’.

‘But I haven’t enough colours’, said Tim without a thought. De Morgan would have smiled and left him to the task. But just recently one of his students, Frederick Guthrie, had asked him about it, and mentioned a successful colouring of England with only four colours. The problem stirred De Morgan’s mathematical imagination.

Is it possible to colour any map with just four colours so that the regions are distinguished? Cartographers may have believed this for centuries but can it be proved rigorously? We can think of any map in the world besides the English county map, such as American states or French départements, and even artificial maps, made up of arbitrary regions and borders. Three colours, though, are not enough.

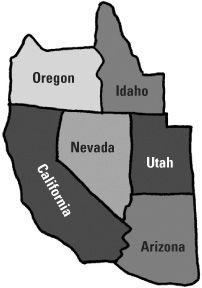
The western states of America

Let’s look at the map of the western states of America. If only blue, green and red were available we could start off by colouring Nevada and Idaho. It does not matter which colour we begin with so we’ll choose blue for Nevada and green for Idaho. So far so good. This choice would mean that Utah must be coloured red, and in turn Arizona green, California red, and Oregon green. This means that both Oregon and Idaho are coloured green so cannot be distinguished. But if we had four colours, with a yellow as well, we could use this to colour Oregon and everything would be satisfactory. Would these four colours – blue, green, red and yellow be sufficient for any map? This question is known as the four-colour problem.

The spread of the problem

Within 20 years of De Morgan recognizing the problem as one of significance, it became known within the mathematical community of Europe and America. In the 1860s, Charles Sanders Peirce, an American mathematician and philosopher, thought he had proved it but there is no trace of his argument.

The problem gained greater prominence through the intercession of the Victorian man of science Francis Galton. He saw publicity value in it and inveigled the eminent Cambridge mathematician Arthur Cayley to write a paper on it in 1878. Unhappily, Cayley was forced to admit that he had failed to obtain a proof, but he observed that it was sufficient to consider only cubic maps (where exactly three countries meet at a point). This contribution spurred on his student Alfred Bray Kempe to attempt a solution. Just one year later Kempe announced he had found a proof. Cayley heartily congratulated him, his proof was published, and he gained election to the Royal Society of London.

What happened next?

Kempe’s proof was long and technically demanding, and though one or two people were unconvinced by it, the proof was generally accepted. There was a surprise ten years later when Durhambased Percy Heawood found an example of a map which exposed a flaw in Kempe’s argument. Though he failed to find his own proof, Heawood showed that the challenge of the four-colour problem was still open. It would be back to the drawing boards for mathematicians and a chance for some new tyro to make their mark. Using some of Kempe’s techniques Heawood proved a five-colour theorem – that any map could be coloured with five colours. This would have been a great result if someone could construct a map that could not be coloured with four colours. As it was, mathematicians were in a quandary: was it to be four or five?

The simple donut or ‘torus’

The basic four-colour problem was concerned with maps drawn on a flat or spherical surface. What about maps drawn on a surface like a donut – a surface more interesting to mathematicians for its shape than its taste. For this surface, Heawood showed that seven colours were both necessary and sufficient to colour any map drawn on it. He even proved a result for a multi-holed donut (with a number, h, holes) in which he counted the number of colours that guaranteed any map could be coloured – though he had not proved these were the minimum number of colours. A table for the first few values of Heawood’s h is:

A torus with two holes

and in general, C = [½(7 + √(1 + 48h))]. The square brackets indicate that we only take the whole number part of the term within them. For example, when h = 8, C = [13.3107. . . ] = 13. Heaward’s formula was derived on the strict understanding that the number of holes is greater than zero. Tantalizingly the formula gives the answer C = 4 if the debarred value h = 0 is substituted.

The problem solved?

After 50 years, the problem which had surfaced in 1852 remained unproved. In the 20th century the brainpower of the world’s elite mathematicians was flummoxed.

Some progress was made and one mathematician proved that four colours were enough for up to 27 countries on a map, another bettered this with 31 countries and one came in with 35 countries. This nibbling process would take forever if continued. In fact the observations made by Kempe and Cayley in their very early papers provided a better way forward, and mathematicians found that they had only to check certain map configurations to guarantee that four colours were enough. The catch was that there was a large number of them – at the early stages of these attempts at proof there were thousands to check. This checking could not be done by hand but luckily the German mathematician Wolfgang Haken, who had worked on the problem for many years, was able to enlist the services of the American mathematician and computer expert Kenneth Appel. Ingenious methods lowered the number of configurations to fewer than 1500. By late June 1976, after many sleepless nights, the job was done and in partnership with their trusty IBM 370 computer, they had cracked the great problem.

The mathematics department at the University of Indiana had a new trumpet to blow. They replaced their ‘largest discovered prime’ postage stamp with the news that ‘four colours suffice.’ This was local pride but where was the general applause from the world’s mathematics community? After all, this was a venerable problem which can be understood by any person of Tiny Tim’s tender years, but for well over a century had teased and tortured some of the greatest mathematicians.

The applause was patchy. Some grudgingly accepted that the job had been done but many remained sceptical. The trouble was that it was a computer-based proof and this stepped right outside the traditional form of a mathematical proof. It was only to be expected that a proof would be difficult to follow, and the length could be long, but a computer proof was a step too far. It raised the issue of ‘checkability’. How could anyone check the thousands of lines of computer code on which the proof depended. Errors in computer coding can surely be made. An error might prove fatal.

That was not all. What was really missing was the ‘aha’ factor. How could anyone read through the proof and appreciate the subtlety of the problem, or experience the crucial part of the argument, the aha moment. One of the fiercest critics was the eminent mathematician Paul Halmos. He thought that a computer proof had as much credibility as a proof by a reputable fortune teller. But many do recognize the achievement, and it would be a brave or foolish person who would spend their precious research time trying to find a counterexample of a map which required five colours. They might well have done pre Appel and Haken, but not afterwards.

After the proof

Since 1976 the number of configurations to be checked has been reduced by a factor of a half and computers have become faster and more powerful. This said, the mathematical world still awaits a shorter proof along traditional lines. Meanwhile the four-colour theorem has spawned significant problems in graph theory and had the subsidiary effect of challenging the mathematician’s very notion of what constitutes a mathematical proof.

the condensed idea

Four colours will be enough

مواضيع ذات صلة

π

Zero

Triangles

Topology

The travelling salesperson

The Riemann hypothesis

The parallel postulate

The normal curve

The diet problem

The birthday problem

Squares and square roots

Sets