


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-2-2016
Date: 28-2-2016
Date: 21-2-2016
|
‘If there are fewer cars on the roads the pollution will be acceptable. Either we have fewer cars on the road or there should be road pricing, or both. If there is road pricing the summer will be unbearably hot. The summer is actually turning out to be quite cool. The conclusion is inescapable: pollution is acceptable.’
Is this argument from the leader of a daily newspaper ‘valid’ or is it illogical? We are not interested in whether it makes sense as a policy for road traffic or whether it makes good journalism. We are only interested in its validity as a rational argument. Logic can help us decide this question – for it concerns the rigorous checking of reasoning.
Two premises and a conclusion
As it stands the newspaper passage is quite complicated. Let’s look at some simpler arguments first, going all the way back to the Greek philosopher Aristotle of Stagira who is regarded as the founder of the science of logic. His approach was based on the different forms of the syllogism, a style of argument based on three statements: two premises and a conclusion. An example is

Above the line we have the premises, and below it, the conclusion. In this example, the conclusion has a certain inevitability about it whatever meaning we attach to the words ‘spaniels’, ‘dogs’ and ‘animals’. The same syllogism, but using different words is
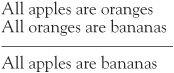
In this case, the individual statements are plainly nonsensical if we are using the usual connotations of the words. Yet both instances of the syllogism have the same structure and it is the structure which makes this syllogism valid. It is simply not possible to find an instance of As, Bs and Cs with this structure where the premises are true but the conclusion is false. This is what makes a valid argument useful.
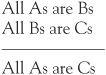
A valid argument
A variety of syllogisms are possible if we vary the quantifiers such as ‘All’, ‘Some’ and ‘No’ (as in No As are Bs). For example, another might be
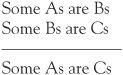
Is this a valid argument? Does it apply to all cases of As, Bs and Cs, or is there a counterexample lurking, an instance where the premises are true but the conclusion false? What about making A spaniels, B brown objects, and C tables? Is the following instance convincing?

Our counterexample shows that this syllogism is not valid. There were so many different types of syllogism that medieval scholars invented mnemonics to help remember them. Our first example was known as BARBARA because it contains three uses of ‘All’. These methods of analysing arguments lasted for more than 2000 years and held an important place in undergraduate studies in medieval universities. Aristotle’s logic – his theory of the syllogism – was thought to be a perfect science well into the 19th century.
Or truth table
Propositional logic
Another type of logic goes further than syllogisms. It deals with propositions or simple statements and the combination of them. To analyse the newspaper leader we’ll need some knowledge of this ‘propositional logic’. It used to be called the ‘algebra of logic’, which gives us a clue about its structure, since George Boole realized that it could be treated as a new sort of algebra. In the 1840s there was a great deal of work done in logic by such mathematicians as Boole and Augustus De Morgan.
And truth table
Let’s try it out and consider a proposition a, where a stands for ‘Freddy is a spaniel’. The proposition a may be True or False. If I am thinking of my dog named Freddy who is indeed a spaniel then the statement is true (T) but if I am thinking that this statement is being applied to my cousin whose name is also Freddy then the statement is false (F). The truth or falsity of a proposition depends on its reference.

Not truth table
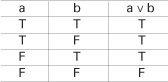
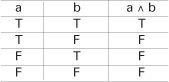
If we have another proposition b such as ‘Ethel is a cat’ then we can combine these two propositions in several ways. One combination is written a V b. The connective V corresponds to ‘or’ but its use in logic is slightly different from ‘or’ in everyday language. In logic, a V b is true if either ‘Freddy is a spaniel’ is true or ‘Ethel is a cat’ is true, or if both are true, and it is only false when both a and b are false. This conjunction of propositions can be summarized in a truth table.
Implies truth table
We can also combine propositions using ‘and’, written as a⋀b, and ‘not’, written as ¬a. The algebra of logic becomes clear when we combine these propositions using a mixture of the connectives with a, b and c like a ⋀ (b Vc) . We can obtain an equation we call an identity:
a⋀(b V c) = (a ⋀ b) V (a V c )
The symbol ≡ means equivalence between logical statements where both sides of the equivalence have the same truth table. There is a parallel between the algebra of logic and ordinary algebra because the symbols Λ and V act similarly to × and + in ordinary algebra, where we have x × (y + z) = (x × y) + (x × z). However, the parallel is not exact and there are exceptions.
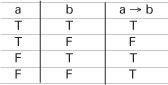
Other logical connectives may be defined in terms of these basic ones. A useful one is the ‘implication’ connective a→b which is defined to be equivalent to ¬ a ⋀ b and has the truth table shown.
Now if we look again at the newspaper leader, we can write it in symbolic form to give the argument in the margin:
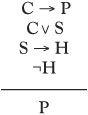

Is the argument valid or not? Let’s assume the conclusion P is false, but that all the premises are true. If we can show this forces a contradiction, it means the argument must be valid. It will then be impossible to have the premises true but the conclusion false. If P is false, then from the first premise C → P, C must be false. As C VS is true, the fact that C is false means that S is true. From the third premise S → H this means that H is true. That is, ¬H is false. This contradicts the fact that ¬H, the last premise, was assumed to be true. The content of the statements in the newspaper leader may still be disputed, but the structure of the argument is valid.
|
V |
or |
|
⋀ |
and |
|
¬ |
not |
|
→ |
implies |
|
∀ |
for all |
|
∃ |
there exists |
Other logics
Gottlob Frege, C.S. Peirce, and Ernst Schröder introduced quantification to propositional logic and constructed a ‘first-order predicate logic’ (because it is predicated on variables). This uses the universal quantifier, ∀, to mean ‘for all’, and the existential quantifier, ∃, to mean ‘there exists’.
Another new development in logic is the idea of fuzzy logic. This suggests confused thinking, but it is really about a widening of the traditional boundaries of logic. Traditional logic is based on collections or sets. So we had the set of spaniels, the set of dogs, and the set of brown objects. We are sure what is included in the set and what is not in the set. If we meet a pure bred ‘Rhodesian ridgeback’ in the park we are pretty sure it is not a member of the set of spaniels.
Fuzzy set theory deals with what appear to be imprecisely defined sets. What if we had the set of heavy spaniels. How heavy does a spaniel have to be to be included in the set? With fuzzy sets there is a gradation of membership and the boundary as to what is in and what is out is left fuzzy. Mathematics allows us to be precise about fuzziness. Logic is far from being a dry subject. It has moved on from Aristotle and is now an active area of modern research and application.
the condensed idea
The clear line of reason




|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|