المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | هندسة تحليلية Analytic Geometry |
 1760
 09:21 صباحاً
التاريخ: 29-12-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 374|
أقرأ أيضاً
التاريخ: 29-12-2015
1985
التاريخ: 13-12-2015
924
التاريخ: 5-11-2015
779
التاريخ: 7-12-2015
8803
|
انها من فروع الرياضيات الأكثر أهمية من غيره , كونها تربط مفاهيم الجبر بمفاهيم الهندسة وتمزج البناء الجبري للرياضيات بالبناء الهندسي لها , مما يتيح لنا تمثيل الرموز والتعابير الجبرية هندسياً .
وتسمى أيضاً هندسة النقاط أو الهندسة الديكارتية لأن موضوع هذه الهندسة قد تبلور وأصبح على ما هو عليه على يد الرياضي والفيلسوف الفرنسي ديكارت ( 1596 – 1650)م التي تنسب إليه .
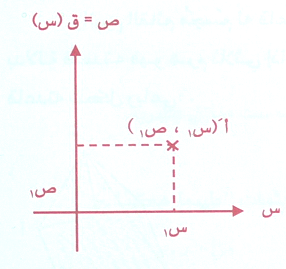
وتبحث هذه الهندسة بشكل خاص في تعيين النقط على المستوى ثنائي الأبعاد والمسمى المستوى الديكارتي كما في الشكل .
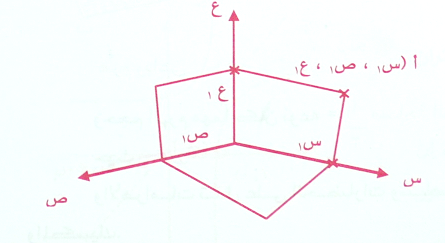
وفي تعيين النقط في الفضاء ثلاثي الأبعاد كما في الشكل .
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
