Bousso’s Generalization

Consider an arbitrary cosmology. Take a space-like region Γ bounded by the space-like boundary ∂Γ. At any point on the boundary we can construct four light rays that are perpendicular to the boundary[6]. We will call these the four branches.Tw o branches go toward the future. One of them is composed of outgoing rays and the other is ingoing. Similarly two branches go to the past. On any of these branches a light ray, together with its neighbors define a positive or negative expansion as we move away from the boundary. In ordinary flat space-time, if ∂Γ is convex the outgoing (ingoing) rays have positive (negative) expansion. However in non-static universes other combinations are possible. For example in a rapidly contracting universe both future branches have negative expansion while the past branches have positive expansion.

If we consider general boundaries the sign of the expansion of a given branch may vary as we move over the surface. For simplicity we restrict attention to those regions for which a given branch has a unique sign. We can now state Bousso’s rule:

From the boundary ∂Γ construct all light sheets which have negative expansion as we move away. These light sheets may terminate at the tip of a cone or a caustic or even a boundary of the geometry. Bousso’s bound states that the entropy passing through these light sheets is less than A/4G where A is the boundary of ∂Γ.

To help visualize how Bousso's construction works we will consider spherically symmetric geometries and use Penrose diagrams to describe them. The Penrose diagram represents the radial and time directions. Each point of such a diagram really stands for a 2-sphere (more generally a (d − 1)-sphere). The four branches at a given point on the Penrose diagram are represented by a pair of 45 degree lines passing through that point. However we are only interested in the branches of negative expansion. For example in Figure 1.1 we illustrate flat space-time and the negative expansion branches of a typical local 2-sphere.I n general as we move around in the Penrose diagram the particular branches which have negative expansion may change. For example if the cosmology initially expands and then collapses, the outgoing future branch will go from positive to negative expansion. Bousso introduced a notation to indicate this. The Penrose diagram is divided into a number of regions depending on which branches have negative expansion. In each region the negative expansion branches are indicated by their directions at a typical point. Thus in Figure 1.2 we draw the Penrose–Bousso (PB) diagram for a positive curvature, matter dominated universe that begins with a bang and ends with a crunch. It consists of four distinct regions. In Region I of Figure 1.2 the expansion of the universe causes both past branches to have negative expansion. Thus we draw light surfaces into the past. These light surfaces terminate on the initial boundary of the

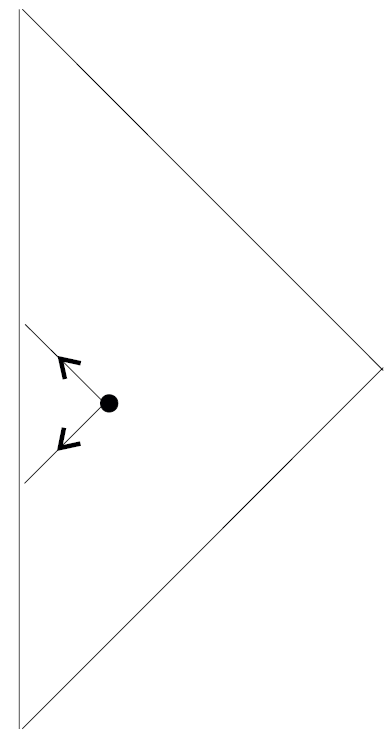
Fig. 1.1. Negative expansion branches of 2-sphere in flat space-time.

geometry and are similar to the truncated cones that we discussed in the flat F.R.W. case. The holographic bound in this case says that the entropy passing through either backward light surface is bounded by the area of the 2-sphere at point p. Bousso's rule tells us nothing in this case about the entropy on space-like surfaces bounded by p.

Now move on to Region II. The relevant light sheets in this region begin on the 2-sphere q and both terminate at the spatial origin. These are untruncated cones and the entropy on both of them is holographically bounded. There is something new in this case. We find that the entropy is bounded on a future light sheet. Now consider a space-like surface bounded by q and extending to the spatial origin (shown in Figure 1.3). It is evident that any matter which passes through the space-like surface must also pass through the future light sheet. By the second law of thermodynamics the entropy on the space-like surface cannot exceed the entropy on the future light sheet. Thus in this case the entropy in a space-like region can be holographically bounded. Therefore, one condition for a space-like bound is that the entropy is bounded by a corresponding future light sheet. With this in mind we return to Region I. For Region I there is no future bound, and therefore the entropy is not bounded on space-like regions with boundary p.

In Region III the entropy bounds are both on future light sheets. Nevertheless there is no space-like bound. The reason is that not all matter

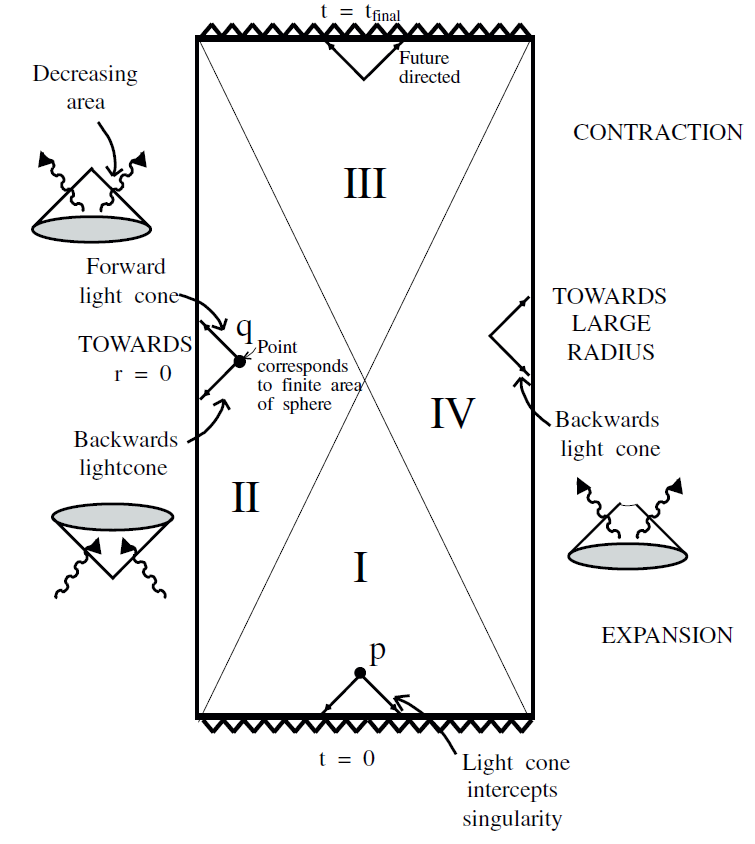
Fig. 1.2. Penrose–Bousso diagram for matter dominated universe.

which pass through space-like surfaces are forced to pass through the future light sheets.

Region IV is identical to Region II with the spatial origin being replaced by the diametrically opposed antipode. Thus we see that there are light-like bounds in all four regions but only in II and IV are there holographic bound on space-like regions. (See Figure 1.3.) Figure 1.4 demonstrates a region that does not satisfy an entropy bound for this cosmology.

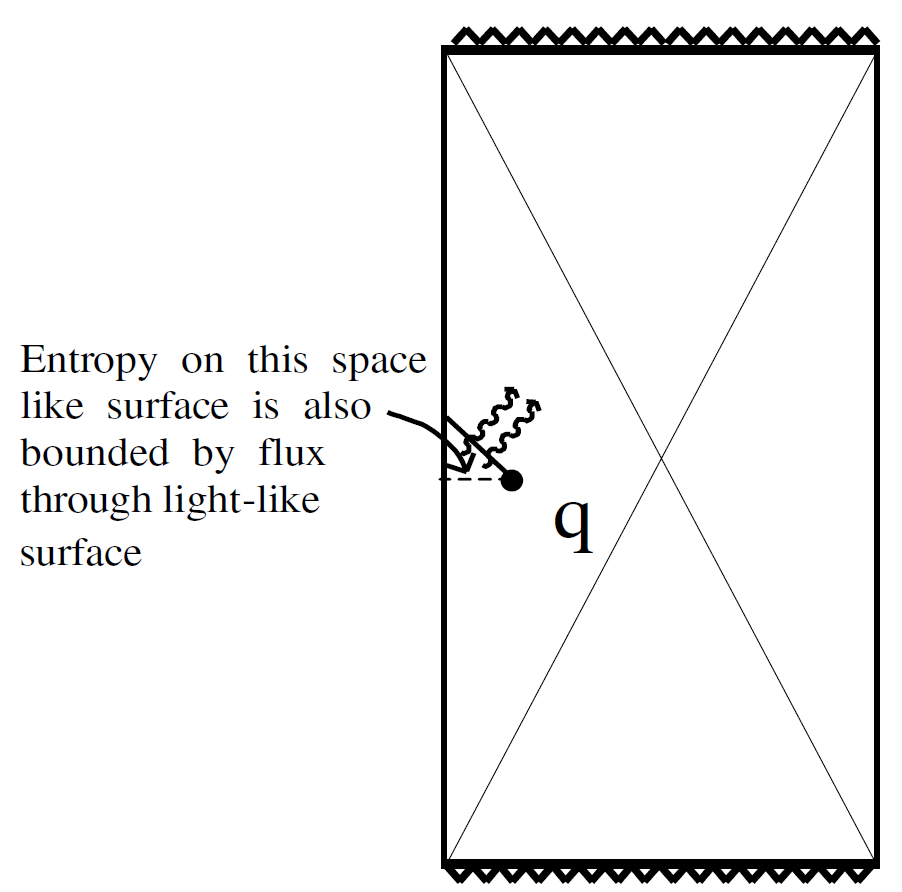
Fig. 1.3. Bounding surfaces for inflowing entropy.

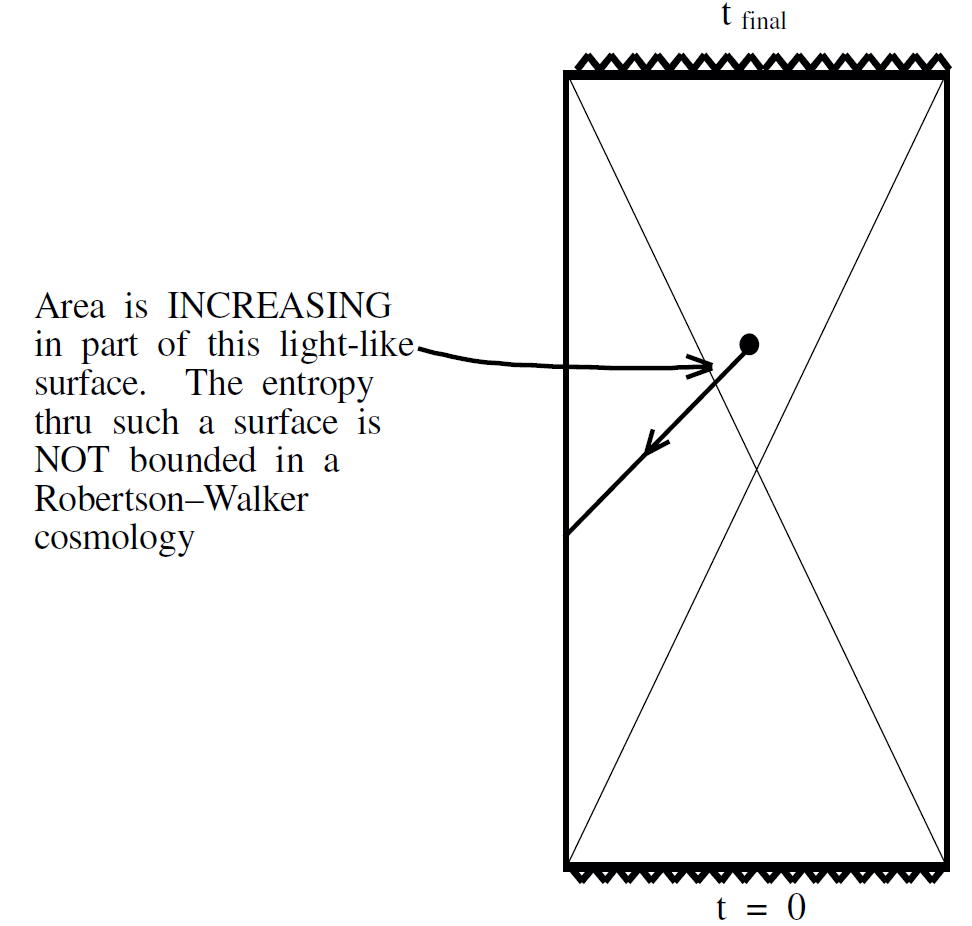
Fig. 1.4. Light-like surface which does not satisfy entropy bound.