المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | شجرة بيانية Tree Diagram |
 5831
 08:48 صباحاً
التاريخ: 15-11-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 170-171|
أقرأ أيضاً
التاريخ: 4-4-2021
1276
التاريخ: 26-2-2021
2906
التاريخ: 29-11-2015
1970
التاريخ: 10-4-2021
1123
|
مع انها شجرة عديمة الثمار , كونها لا شجرة تفاح ولا شجرة برتقال , ولا أي شجرة من أشجار الفواكه على الإطلاق , إلا انها مفيدة كوسيلة للتوضيح في موضوع الاحتمال , إذ عن طريقها نستطيع معرفة عدد عناصر الفضاء العيني وأوميجا Ω للتجربة العشوائية ثم ترتيبها بشكل دقة وإتقان , أغصانها ترتبط ببعضها البعض على الدوام إلا الأغصان الأخيرة والتي تسمى الاغصان السائبة كونها لا ترتبط بأخرى من الامام , حيث عدد هذه الأغصان يساوي عدد عناصر الفضاء العيني بالتمام ودونك المثال ؛
ارم قطعة نقدٍ ثلاث مرات متتالية في الهواء ثم اكتب الفضاء العيني لهذه للتجربة العشوائية مستعيناً بالشجرة البيانية .
عدد عناصر الفضاء العيني = ع(Ω) =2ن حيث ن عدد مرات التكرار التجربة وهنا = 3 , العدد 3 هو عدد أوجه قطعة النقد { ص , ك} .
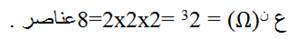
والشكل كالتالي :
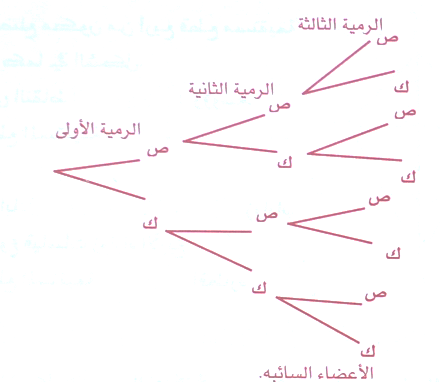
ومنها فإن عدد الأغصان السائبة = 8 فعدد عناصر Ω=8 وبالتمام هي وبالترتيب .
Ω = { ص ص ص , ص ص ك , ص ك ص , ص ك ك , ك ص ص , ك ص ك , ك ك ص , ك ك ك }
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|
