المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | تكامل بالكسور الجزئية Integration by partid Fractions |
 16095
 11:28 صباحاً
التاريخ: 3-11-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 90|
أقرأ أيضاً
التاريخ: 1-9-2019
3688
التاريخ: 25-3-2019
1402
التاريخ: 3-9-2019
2315
التاريخ: 4-9-2019
1320
|
أنها طريقة لتكامل الاقترانات النسبية والتي بسطها لا يظهر في مشتقة مقامها , إذ يجزأ الاقتران النسبي إلى اقترانات جزئية أخرى بحيث يصبح بسط كل منها يظهر في مشتقة مقامه ومن تم يتم تطبيق القاعدة
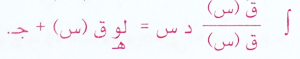
شرط أن يكون مقام الاقتران النسبي جذر حدود وتربيعي وقابل للتحليل إلى اقترانات خطية غير متطابقة وإلا فالطريقة معقدة وخارجة عن نطاق الرياضيات .
مثال :
|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|
