


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | التفسير الهندسي للمشتقة الأولى Geometric Interpretation for the First Derivative |
|
|
|
أقرأ أيضاً
التاريخ: 29-10-2015
التاريخ: 2-11-2015
التاريخ: 29-10-2015
التاريخ: 16-12-2015
|
يرتبط هذا التفسير بالهندسة التحليلية حيث ان
حـ ص ص2 – ص1 ق(س2) – ق(س1)
م القاطع = ـــــــــــ = ـــــــــــــــــــــــــــ = ــــــــــــــــــــــــــــــ
حـ س س2 – س1 س2 – س1
وعندما حـ س ـــــــ صفر
حـ س
فإن م المماس = نها ــــــــــــــ ق(س1) = ظا هــ
حـ س
حـ س ــــــ صفر
حيث هـ الزاوية التي يضعها المماس مع الاتجاه الموجب لمحور السينات كما في الشكل :
وحيث ن( س1 , ص1)
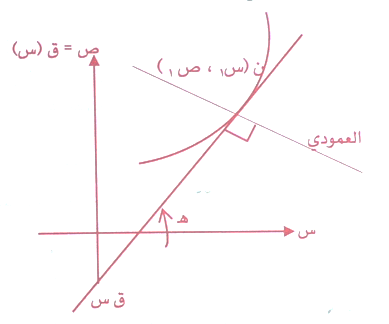
هي نقطة التماس وعندها فإن معادلة التماس :
ص – ص1 = ق(س1)
(س2 – س1) ومعادلة العمودي عليه هي
ــ 1 ــ 1
ص – ص1 = ــــــــــــــــ (س2 – س1) جيت م العمودي = ـــــــــــــــ
ق(س1) ق(س1)
فإذا كان ق(س) = س3 لوجد معادلة المماس والعمودي عندما س = 2 كما في الشكل : الاحداثي الصادي ص1 = (2) = 8
نقطة التماس = (2 , 8)
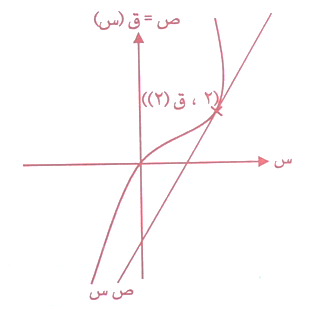
م مماس = قَ (س1)
= 3(س1)2 = 3(2)2 = 12
ــ 1
م العمودي = ـــــــــــــــ
12
معادلة المماس :
ص – 8 = 12 (س – 2)
ص – 8 = 12 س – 24
ص = 12س – 24 + 8
ص = 12س – 16
معادلة العمودي :
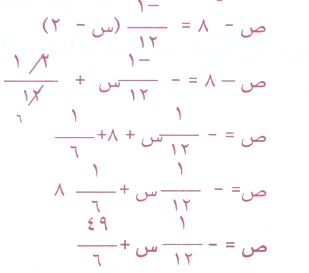



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|