


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2023-06-14
التاريخ: 2025-03-19
التاريخ: 2023-07-20
التاريخ: 2023-10-12
|
Now we shall calculate the total energy radiated by an accelerating charge. To keep the discussion general, we shall take the case of a charge accelerating any which way, but nonrelativistically. At a moment when the acceleration is, say, vertical, we know that the electric field that is generated is the charge multiplied by the projection of the retarded acceleration, divided by the distance. So, we know the electric field at any point, and we therefore know the square of the electric field and thus the energy ϵ0cE2 leaving through a unit area per second.
The quantity ϵ0c appears quite often in expressions involving radiowave propagation. Its reciprocal is called the impedance of a vacuum, and it is an easy number to remember: it has the value 1/ϵ0c=377 ohms. So, the power in watts per square meter is equal to the average of the field squared, divided by 377.
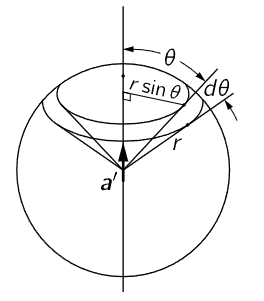
Fig. 32–1. The area of a spherical segment is 2πr sinθ ⋅ r dθ.
Using our expression (29.1) for the electric field, we find that
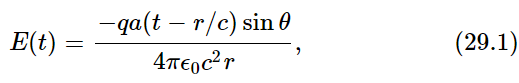

is the power per square meter radiated in the direction θ. We notice that it goes inversely as the square of the distance, as we said before. Now suppose we wanted the total energy radiated in all directions: then we must integrate (32.2) over all directions. First, we multiply by the area, to find the amount that flows within a little angle dθ (Fig. 32–1). We need the area of a spherical section. The way to think of it is this: if r is the radius, then the width of the annular segment is r dθ, and the circumference is 2πr sinθ, because r sinθ is the radius of the circle. So, the area of the little piece of the sphere is 2πr sinθ times r dθ:

By multiplying the flux [(32.2), the power per square meter] by the area in square meters included in the small angle dθ, we find the amount of energy that is liberated in this direction between θ and θ+dθ; then we integrate that over all the angles θ from 0 to 180∘:

By writing sin3θ = (1−cos2θ) sinθ it is not hard to show that 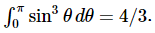 Using that fact, we finally get
Using that fact, we finally get

This expression deserves some remarks. First of all, since the vector a′ had a certain direction, the a′2 in (32.5) would be the square of the vector a′, that is, a′⋅a′, the length of the vector, squared. Secondly, the flux (32.2) was calculated using the retarded acceleration; that is, the acceleration at the time at which the energy now passing through the sphere was radiated. We might like to say that this energy was in fact liberated at this earlier time. This is not exactly true; it is only an approximate idea. The exact time when the energy is liberated cannot be defined precisely. All we can really calculate precisely is what happens in a complete motion, like an oscillation or something, where the acceleration finally ceases. Then what we find is that the total energy flux per cycle is the average of acceleration squared, for a complete cycle. This is what should really appear in (32.5). Or, if it is a motion with an acceleration that is initially and finally zero, then the total energy that has flown out is the time integral of (32.5).
To illustrate the consequences of formula (32.5) when we have an oscillating system, let us see what happens if the displacement x of the charge is oscillating so that the acceleration a is −ω2x0eiωt. The average of the acceleration squared over a cycle (remember that we have to be very careful when we square things that are written in complex notation—it really is the cosine, and the average of cos2 ωt is one-half) thus is
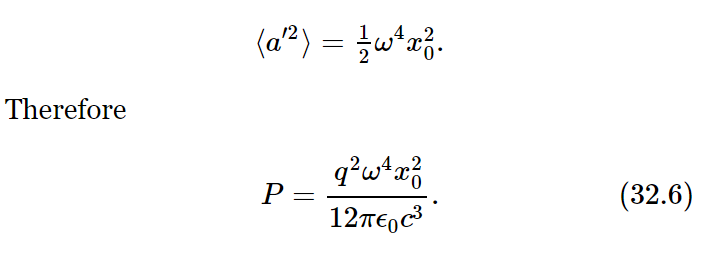
The formulas we are now discussing are relatively advanced and more or less modern; they date from the beginning of the twentieth century, and they are very famous. Because of their historical value, it is important for us to be able to read about them in older books. In fact, the older books also used a system of units different from our present mks system. However, all these complications can be straightened out in the final formulas dealing with electrons by the following rule: The quantity q2e/4πϵ0, where qe is the electronic charge (in coulombs), has, historically, been written as e2. It is very easy to calculate that e in the mks system is numerically equal to 1.5188×10−14, because we know that, numerically, qe=1.60206×10−19 and 1/4πϵ0=8.98748×109. Therefore, we shall often use the convenient abbreviation

If we use the above numerical value of e in the older formulas and treat them as though they were written in mks units, we will get the right numerical results. For example, the older form of (32.5) is P=2/3 e2a′2/c3. Again, the potential energy of a proton and an electron at distance r is q2e/4πϵ0r or e2/r, with e=1.5188×10−14 (mks).



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|