
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Addition and multiplication
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 22
2024-03-09
1773
In our study of oscillating systems we shall have occasion to use one of the most remarkable, almost astounding, formulas in all of mathematics. From the physicist’s point of view we could bring forth this formula in two minutes or so, and be done with it. But science is as much for intellectual enjoyment as for practical utility, so instead of just spending a few minutes on this amazing jewel, we shall surround the jewel by its proper setting in the grand design of that branch of mathematics which is called elementary algebra.
Now you may ask, “What is mathematics doing in a physics lecture?” We have several possible excuses: first, of course, mathematics is an important tool, but that would only excuse us for giving the formula in two minutes. On the other hand, in theoretical physics we discover that all our laws can be written in mathematical form; and that this has a certain simplicity and beauty about it. So, ultimately, in order to understand nature it may be necessary to have a deeper understanding of mathematical relationships. But the real reason is that the subject is enjoyable, and although we humans cut nature up in different ways, and we have different courses in different departments, such compartmentalization is really artificial, and we should take our intellectual pleasures where we find them.
Another reason for looking more carefully at algebra now, even though most of us studied algebra in high school, is that that was the first time we studied it; all the equations were unfamiliar, and it was hard work, just as physics is now. Every so often it is a great pleasure to look back to see what territory has been covered, and what the great map or plan of the whole thing is. Perhaps some day somebody in the Mathematics Department will present a lecture on mechanics in such a way as to show what it was we were trying to learn in the physics course!
The subject of algebra will not be developed from the point of view of a mathematician, exactly, because the mathematicians are mainly interested in how various mathematical facts are demonstrated, and how many assumptions are absolutely required, and what is not required. They are not so interested in the result of what they prove. For example, we may find the Pythagorean theorem quite interesting, that the sum of the squares of the sides of a right triangle is equal to the square of the hypotenuse; that is an interesting fact, a curiously simple thing, which may be appreciated without discussing the question of how to prove it, or what axioms are required. So, in the same spirit, we shall describe qualitatively, if we may put it that way, the system of elementary algebra. We say elementary algebra because there is a branch of mathematics called modern algebra in which some of the rules such as ab=ba, are abandoned, and it is still called algebra, but we shall not discuss that.
To discuss this subject we start in the middle. We suppose that we already know what integers are, what zero is, and what it means to increase a number by one unit. You may say, “That is not in the middle!” But it is the middle from a mathematical standpoint, because we could go even further back and describe the theory of sets in order to derive some of these properties of integers. But we are not going in that direction, the direction of mathematical philosophy and mathematical logic, but rather in the other direction, from the assumption that we know what integers are and we know how to count.
If we start with a certain number a, an integer, and we count successively one unit b times, the number we arrive at we call a+b, and that defines addition of integers.
Once we have defined addition, then we can consider this: if we start with nothing and add a to it, b times in succession, we call the result multiplication of integers; we call it b times a.
Now we can also have a succession of multiplications: if we start with 1 and multiply by a, b times in succession, we call that raising to a power: ab.
Now as a consequence of these definitions it can be easily shown that all of the following relationships are true:
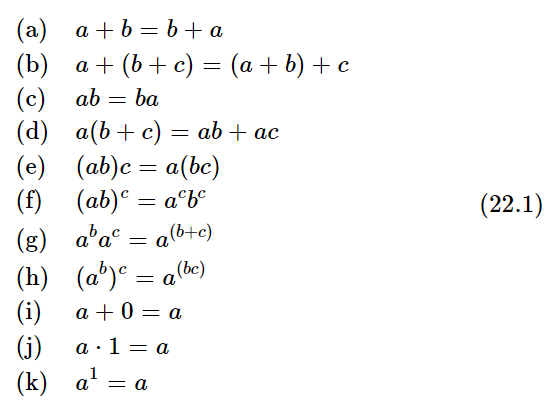
These results are well known and we shall not belabor the point, we merely list them. Of course, 1 and 0 have special properties; for example, a+0 is a, a times 1=a, and a to the first power is a.
In this discussion we must also assume a few other properties like continuity and ordering, which are very hard to define; we will let the rigorous theory do it. Furthermore, it is definitely true that we have written down too many “rules”; some of them may be deducible from the others, but we shall not worry about such matters.
 الاكثر قراءة في الفيزياء الرياضية
الاكثر قراءة في الفيزياء الرياضية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















