Born: about 220 in Wei, China
Died: about 280 in China

Liu Hui lived in the Kingdom of Wei so it is likely that he worked in what is now the Shansi province in north-central China. The Kingdom of Wei had come about after the Han Empire, which lasted from around 200 BC to 220 AD, collapsed. However, the collapse of the Han Empire led to three Kingdoms coming into existence for, in addition to the Kingdom of Wei, two former Han generals set up Kingdoms, one to the south of the Yangtze and one in the west of China in the present Szechwan Province. This situation lasted for about sixty years, from 220 to 280, which must have been almost exactly the period of Liu Hui's life.

The period of the Three Kingdoms was one of almost constant warfare and political intrigue. However this fascinating period is now thought of as the most romantic in all of Chinese history. What influence the events of the period had on Liu Hui is unknown, for nothing is known of his life except that he wrote two works. One was an extremely important commentary on the Jiuzhang suanshu or, as it is more commonly called Nine Chapters on the Mathematical Art, and the other was a much shorter work called Haidao suanjing or Sea Island Mathematical Manual. That no record of Liu Hui's life was written, or at least if it was it was not considered worth preserving, does not mean that he was particularly obscure during his lifetime. Although mathematics was an important topic in China, nevertheless being a mathematician seems to have been considered an occupation of minor importance. As a consequence many Chinese mathematical works are anonymous.

The only precise information about Liu Hui comes from a later work which states that he wrote his commentary on the Nine Chapters on the Mathematical Art in the fourth year of the era of the Jingyuan reign of Prince Chenliu of the Wei, which gives a date of 263 AD. He did not date his commentary, however, so even this "fact" is unconfirmed. One piece of information he gives us about his life in the Preface of the book is:-

I read the Nine Chapters as a boy, and studied it in full detail when I was older.

What exactly was is the text that Liu Hui is commenting on? It was a practical handbook of mathematics meant to provide methods to be used to solve everyday problems of engineering, surveying, trade, and taxation. How old was the original text? This is a hard question to which historians have found no definite answer. Liu Hui himself believed that the text which he was commentating on was originally written around 1000 BC but incorporating much material of later eras. He writes in the Preface:-

In the past, the tyrant Qin burnt written documents, which led to the destruction of classical knowledge. Later, Zhang Cang, Marquis of Peiping and Geng Shouchang, Vice-President of the Ministry of Agriculture, both became famous through their talent for calculation. Because the ancient texts had deteriorated, Zhang Cang and his team produced a new version removing the poor parts and filling in the missing parts. Thus, they revised some parts, with the result that these were different from the old parts ...

Let us give some dates for the events Liu Hui describes. The Qin dynasty preceded the Han dynasty and it was the Qin ruler Shih Huang Ti who tried to reform education by destroying all earlier learning. He ordered all books to be burnt in 213 BC and Zhang Cang, who Liu Hui refers to, did his reconstruction around 170 BC. Most historians, however, would not believe that the original text of the Nine Chapters was nearly as old as Liu Hui believed. We discuss such issues in the article on The Nine Chapters on the Mathematical Art. In fact most historians think that Liu Hui was quite wrong in what he wrote, for it is now thought that the text originated around 200 BC after the burning of the books by Shih Huang Ti.

Let us examine the mathematical contributions that Liu Hui made in writing his commentary. First we should note that he introduced a different approach to mathematics from that of the text on which he was commentating. The original text gave methods to solve various problems, but the methods were merely prescriptions without justification. What Liu Hui added was a more mathematical approach in providing at least principles on which the calculations are based. His methods are not exactly "proofs" in our understanding of a mathematical proof today. They are more the type of brief explanation that a mathematician will give to convince you that if you wanted to you could construct a proof. Liu Hui also shows that he understands that some of the methods of the original text are approximations, and he investigates the accuracy of the approximations. There is also evidence that he is beginning to understand concepts associated with early work on the differential and integral calculus.

As an example let us look at the contribution Liu Hui made to finding a good approximation to π. This appears in the first chapter of the Nine Chapters. He found a recurrence relation to express the length of the side of a regular polygon with 3 × 2ⁿ sides in terms of the length of the side of a regular polygon with 3 × 2^n-1 sides. This is achieved with an application of Pythagoras's theorem, which Liu Hui knew as the Gougu theorem.

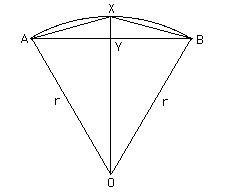
In the diagram we have a circle of radius r with centre O. We know AB, it is p_n-1 , the length of the side of a regular polygon with 3×2^n-1 sides, so AY has length p_n-1/2. Thus OY has length

√(r² - (p_n-1/2)²).

Then YX has length r - √[r² - (p_n-1/2)²].

But now we know AY and YX so we can compute AX using the Gougu theorem (Pythagoras) to be

√{r[2r - √(4r - p_n-1²)]}.

Then p_n= AX is the length of a side of a regular polygon with N = 3 × 2ⁿ sides.

Putting r = 1 and taking n = 1 gives a regular hexagon of side p₆= 1. Then the perimeter of the hexagon is 6p₁= 6 giving an approximate value of π as 6p₁/2 = 3 (assuming the circumference of the circle is approximately the perimeter of the hexagon and using π = circumference/diameter).

In general we obtain an approximate value of π as N p_n/2. Larger values of n give more accurate values of π. Liu Hui used the approximation 3.14 which he obtained from taking n = 5, in other words using a regular polygon of 96 sides. He did not, like Archimedes, find bounds by using an inscribed as well as a circumscribed circle.

We iterate Liu Hui's procedure using a modern computer algebra program to obtain:

n = 1, N = 6, p_n=1, N p_n/2 =3

n = 2, N =12, p_n=0.5176380900, N p_n/2 =3.105828540

n = 3, N = 24, p_n=0.2610523842, N p_n/2 =3.132628610

n = 4, N = 48, p_n=0.1308062584, N p_n/2 =3.139350202

n = 5, N = 96, p_n=0.06543816562, N p_n/2 =3.141031950

n = 6, N = 192, p_n=0.03272346325, N p_n/2 =3.141452472

n = 7, N = 384, p_n=0.01636227920, N p_n/2 =3.141557606

n = 8, N = 768, p_n=0.008181208047, N p_n/2 =3.141583890

n = 9, N = 1536, p_n= .004090612582, N p_n/2 =3.141590463

n = 10, N = 3072, p_n=0.002045307359, N p_n/2 =3.141592104

n = 11, N = 6144, p_n=0.001022653813, N p_n/2 =3.141592514

In fact Liu Hui stopped one step short of our computer calculation, for he also obtained the better approximation from n = 3072, namely 3.14159. As well as the approximate value based on an approximation for π, Liu was able to show that:-

... multiplying half the diameter and half the circumference, one gets the area.

We must emphasise that, of course, Liu Hui did not use algebraic notation as we have done above, nor did he use the number system that we have used. However, the procedure he presented shows that he understood the iterative process we have described. He also understood the notion of a limit.

Other interesting examples of Liu Hui's contributions to the Nine Chapters on the Mathematical Art is in Chapter 5 on engineering works, where he computes the volume of various solids such as a prism, pyramid, tetrahedron, wedge, cylinder, cone and frustum of a cone. He fails, however, to find the volume of a sphere which he says he leaves to a future mathematician to compute. In Chapter 8 he looks at simultaneous linear equations and computes with both positive and negative numbers.

The other work which we mentioned above by Liu Hui is Haidao suanjing or Sea Island Mathematical Manual. This is a small work consisting of nine problems and it was originally written as part of his commentary on Chapter Nine of the Nine Chapters but later removed and made into a separate work by later editors. It shows how to use the Gougu theorem (Pythagoras theorem) to calculate heights of objects and distances to objects which cannot be measured directly. The first problem, which illustrates the style, concerns the height and distance to an island in the sea. It gives its name to the book. 

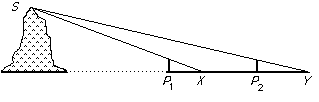
P₁ and P₂ are poles 5 pu high and 1000 pu apart. When viewed from X at ground level, 123 pu behind P₁, the summit S of the island is in line with the top of P₁. Similarly when viewed from Y at ground level, 127 pu behind P₂, the top of the island is in line with the top of P₂. Calculate the height of the island and its distance from P₁. 
[Note: 1 pu is about 2 metres.]

Suppose the poles are of height h and the distance between the poles is d. Liu Hui gives the height of the island as h × d/(P₂Y-P₁X) + h and the distance to it to be P₁X × d/(P₂Y-P₁X). 
He then gives: height of the island: 1255 pu; distance from P₁ to the island: 30750 pu.

Other problems in this work are the height of a tree on the side of a mountain, the distance to a square town, the depth of a gorge, the height of a tower on a hill, the width of a river, the depth of a valley with a lake at the bottom, the width of a ford viewed from a hill, and the size of a town seen from a mountain.

Since we have no information about Liu Hui's life, can we at least deduce some information about him from his work? Firstly we can see that he is an outstanding mathematician with a deep understanding of difficult concepts. He is also highly original, coming up with ideas which rank him among the leading mathematicians of all time. But we can deduce more: as the authors of [4] write:-

The techniques Liu employed are typical of a teacher of skill, patience and tireless zeal.

Liu Hui was a learned man, not only having great expertise in mathematics but also being familiar with the literary and historical classics of China. He could write with clarity and also with style, quoting from a wide variety of sources.

We can also see that he was a modest man who never claimed results of which he was not fully confident, preferring to write:-

Let us leave the problem to whoever can tell the truth.

1. H Peng-Yoke, Biography in Dictionary of Scientific Biography (New York 1970-1990). 
   http://www.encyclopedia.com/doc/1G2-2830902643.html

Books:

1. J-C Martzloff, A history of Chinese mathematics (Berlin-Heidelberg, 1997).
2. J-C Martzloff, Histoire des mathématiques chinoises (Paris, 1987).
3. K Shen, J N Crossley and A W-C Lun, The nine chapters on the mathematical art : Companion and commentary (Beijing, 1999).

Articles:

1. T S Ang and F J Swetz, A Chinese mathematical classic of the third century : the 'Sea island mathematical manual' of Liu Hui, Historia Math. 13 (2) (1986), 99-117.
2. S S Bai, A re-examination of a ring area problem in the 'Jiu zhang suanshu' (Chinese), Beijing Shifan Daxue Xuebao 30 (1) (1994), 139-142.
3. E I Berezkina (trs.), Two texts of Liu Hui on geometry (Russian), in Studies in the history of mathematics, No. 19 (Russian) (Moscow, 1974), 231-273.
4. K Chemla, Different concepts of equations in 'The nine chapters on mathematical procedures' and in the commentary on it by Liu Hui (3rd century), Historia Sci. (2) 4 (2) (1994), 113-137.
5. K Chemla, Relations between procedure and demonstration : Measuring the circle in the 'Nine chapters on mathematical procedures' and their commentary by Liu Hui (3rd century), in History of mathematics and education: ideas and experiences (Essen, 1992) (1996), 69-112.
6. C Cullen, Learning from Liu Hui? A different way to do mathematics, Notices Amer. Math. Soc. 49 (7) (2002), 783-790. 
   http://www.ams.org/notices/200207/comm-cullen.pdf
7. J W Dauben, The 'Pythagorean theorem' and Chinese mathematics : Liu Hui's commentary on the gou-gu theorem in Chapter Nine of the 'Jiu zhang suan shu', in Amphora (Basel, 1992), 133-155.
8. Y Z Dong and Y Yao, The mathematical thought of Liu Hui (Chinese), Qufu Shifan Daxue Xuebao Ziran Kexue Ban 13 (4) (1987), 99-108.
9. L S Feng, 'Jiu zhang suanshu' and Hui Liu's theory of similar right triangles (Chinese), in Collected research papers on the history of mathematics, Vol. 1 (Chinese) (Hohhot, 1990), 37-45.
10. D W Fu, Why did Liu Hui fail to derive the volume of a sphere?, Historia Math. 18 (3) (1991), 212-238.
11. S C Guo, Liu Hui's great contributions to mathematics : celebrating the 1720th anniversary of his commentary on the 'Jiu zhang suanshu' (Chinese), Math. Practice Theory (3) (1983), 75-79.
12. X H Guo, On Liu Hui's 'qiyan method' (Chinese), J. Central China Normal Univ. Natur. Sci. 20 (3) (1986), 400-408.
13. W S Horng, How did Liu Hui perceive the concept of infinity : a revisit, Historia Sci. (2) 4 (3) (1995), 207-222.
14. D Liu, A comparison of Archimedes' and Liu Hui's studies of circles, in Chinese studies in the history and philosophy of science and technology 179 (Dordrecht, 1996), 279-287.
15. R Mei, Liu Hui's theories of mathematics, in Chinese studies in the history and philosophy of science and technology 179 (Dordrecht, 1996), 243-254.
16. S K Mo, 'Jiuzhang suanshu' ('Nine chapters on the mathematical art') and Liu Hui's commentary (Chinese), Stud. Hist. Nat. Sci. 19 (2) (2000), 97-113.
17. H H Shou, L G Liu and G J Wang, An offset approximation algorithm based on Liu Hui's circle subdivision method (Chinese), Appl. Math. J. Chinese Univ. Ser. A 17 (1) (2002), 105-112.
18. P D Straffin Jr, Liu Hui and the first golden age of Chinese mathematics, Math. Mag. 71 (3) (1998), 163-181.
19. A Volkov, Calculation of pi in ancient China : from Liu Hui to Zu Chongzhi, Historia Sci. (2) 4 (2) (1994), 139-157.
20. D B Wagner, A proof of the Pythagorean theorem by Liu Hui (third century AD), Historia Math. 12 (1) (1985), 71-73.
21. D B Wagner, An early Chinese derivation of the volume of a pyramid : Liu Hui, third century AD, Historia Math. 6 (2) (1979), 164-188.
22. X Q Wang, Elementary studies on pi in France in the 17th - 19th centuries and Liu Hui's cyclotomic rule (Chinese), J. Zhejiang Univ. Sci. Ed. 30 (1) (2003), 1-6.
23. Z W Xi and S L Zhang, On the characteristic of the dialectical thought of the 'Jiu zhang suanshu' and Hui Liu's commentary (Chinese), Qufu Shifan Daxue Xuebao Ziran Kexue Ban 19 (4) (1993), 103-110.
24. S C Yang, 'Ratio' and 'power' in Hui Liu's commentary on the 'Jiu zhang suan shu' ('Arithmetic in nine chapters') (Chinese), Dongbei Shida Xuebao (4) (1990), 39-43.